点集求最小包围盒OBB算法 |
您所在的位置:网站首页 › html盒子代码 › 点集求最小包围盒OBB算法 |
点集求最小包围盒OBB算法
|
需求分析
在过去的开发中,客户端和服务端都使用的是手动编辑逻辑包围盒,但这是一个费时费力的工作。随着技术发展,骨骼包围盒这种简化编辑流程,表现效果又好的方式应用开来,新的需求也就出来了。 游戏客户端为了表现效果好,使用的是骨骼包围盒,而且是一个持续区间,而服务端并不支持,服务端只支持瞬时的逻辑包围盒。那么服务端在需要做包围盒判定和校验的时候,需要重新再设置一套逻辑包围盒,与客户端形成一一对应。这样又回到了老路上,并不可取。 所以,由骨骼包围盒绘制逻辑包围盒的需求就出来了——将持续一段时间的骨骼包围盒扫过的空间转化为一个瞬时的逻辑包围盒。 分析实现在客户端,骨骼包围盒分三种——球体、胶囊体、立方体 在服务器,逻辑包围盒分多钟——立方体、圆柱、胶囊体、扇体、球体等
上图展示了其他类型包围盒的契合程度,很明显,带有旋转角度的立方体,也就是OBB是契合度最高的。OBB具有三个维度的长宽高和三个维度的旋转patch,yaw,roll,能够最大程度地还原骨骼包围盒范围,比其他类型的逻辑包围盒冗余是更小的。 那问题转换为如何将球体、胶囊体、立方体转换为立方体OBB,这里分2类讨论。 对球和胶囊体可以归为一类,先将其半径看成是零,算出立方体OBB后再对长宽高加上2倍半径值。那么原始数据就变成了1个点(球变为了点)的集合和2个点和1条线(胶囊体变成了线)的集合。 对立方体,原始数据是8个点和12条线的集合。 如果一个包围盒包含了所有的点,那么必然包含所有点之间的连线。这在数学上非常容易证明。 所以问题转换为点集求最小包围盒OBB的算法问题 执行流程
上图中蓝点为点集,红框为点集的OBB,青框为加上半径后的OBB 按照上述逻辑,流程总结为三步: 通过动态模拟骨骼包围盒在时间段内的运动轨迹,获取轨迹形成的点集和半径依据点集,按照算法求出最小包围盒OBB将OBB和半径转换为逻辑包围盒保存第1步和第3部,逻辑比较简单,就不展开讲了,本文主要讲第2步的算法问题。 算法设计注:下文所指,都是三维空间,虽然算法也适用于二维空间 本算法不是本人发明,而是查阅了资料。这只是一种拟合比较高的算法,并非绝对的最优解,而是相对最优解。何为相对最优解?就是你也许能找到更小的包围盒,但这个算法已经达到完全可用的程度。 算法整体思路是通过点集找一个方向,这个方向上点集的排布是最密集的。 如何定义最密集呢?统计学上以方差作为评估标准,衍生出协方差和协方差矩阵 如何定义这个方向?这个方向也就是我们需要求的包围盒OBB的旋转 AABB和OBB
AABB(Axis-aligned bounding box)轴对齐包围盒,OBB(Oriented bounding box)有向包围盒。顾名思义, AABB指垂直于坐标轴的包围盒,参数包含空间位置,长宽高 OBB指带有旋转的包围盒,参数包含空间位置,长宽高,旋转 根据定义,OBB就是AABB的旋转,那反过来,我们求OBB,也可以转换为将点集转换到AABB空间下,所得的AABB最小。 方差、协方差和协方差矩阵
说了那么多,跟我们的协方差矩阵有什么关系呢? 协方差矩阵定义了我们数据的强度(方差)和方向(协方差)。因此,如果我们想用一个向量和它的大小来表示协方差矩阵,我们应该简单地尝试找到指向数据最大方向上的向量,其大小等于这个方向上的强度(方差) 按照上面的定义,我们就求得了特征值和特征向量。那么有什么用呢? 这里的特征向量就是我们求的线性变换矩阵 OBB的中心和长宽高我们已经有了线性变换矩阵,将原始点转换到AABB空间,然后可以求出立方体OBB的中心点和长宽高了
上图中蓝点为原始轨迹点集,红点为蓝点经过线性变换矩阵转换后的AABB点集。 依据AABB点集,可以通过求三个轴的最大值和最小值,得到AABB中心点,AABB长宽高。 按照AABB与OBB的旋转,这里AABB长宽高就是OBB的长宽高,但AABB中心点并不是OBB的中心点。 为什么中心点不是同一个呢? 由于我们求的线性变换矩阵不包含位移变化,将蓝点转换的时候,同时将中心点也进行了转换。所以将AABB的中心点进行一次反转换,就得到OBB的中心点了。 Tip:你有没有发现红点所在AABB,Z轴大于Y轴,Y轴大于X轴。笔者知道跟特征向量的收敛有关,并没有证明为什么是这样。 变换矩阵转欧拉角我们已经求得了OBB的中心点,长宽高和变换矩阵。那如何将变换矩阵转换到旋转的数据表示呢? 游戏中表示旋转的方式有很多种,一般有欧拉角、四元数、旋转轴等。但最常见的还是欧拉角。 欧拉角,不同于其他表示方式,有左手系与右手系的区别,还有顺规的区别。 我们定义旋转矩阵 定义每个轴的旋转(右手系) 如果以右手系,X-Y-Z顺规,我们能得到旋转矩阵
则可以如下表示欧拉角(不考虑万向节锁):
然后按照公式导出欧拉角就可以了 尴尬的反射矩阵测试上述逻辑后,发现算法有50%是正确的,有50%出现下面的情况 上图中红色是算法的结果,青色是正确的结果 通过查看空间结构,发现欧拉角的z轴旋转roll出现了正负号的问题,也就是roll轴的旋转有时候需要负号,有时候不需要。原因是什么呢? 查阅了大量资料,并没有结果,一度怀疑欧拉角计算出了问题。 一个无意间,计算det(rotate_matrix)(旋转矩阵的行列式)等于-1,不对呀,旋转矩阵行列式为+1啊。 原因找到啦!这个线性变换矩阵有旋转矩阵和反射矩阵。 线性变换矩阵,包含三种变换——位移变换、旋转变换和反射变换 如果行列式是1则是旋转矩阵,如果行列式是-1则是反射矩阵(可能包含旋转) 实对称矩阵的特征向量存在正交矩阵,正交矩阵的行列式为±1。 而协方差矩阵就是实对称矩阵,所以我们求得的线性变换矩阵包含了旋转变换和反射变换 我们根据线性变换矩阵行列式是否是-1来设置roll的旋转角是否添加负号。 按照算出的欧拉角,就获得可如下的结果 上图中蓝点是原始变换矩阵结果,紫红点是欧拉角转换的结果 图中的欧拉角结果与原始结果并不一致,原因是原始变换矩阵带有一个Z轴的反射,而欧拉角旋转矩阵没有。 也就是说,其构造的欧拉角旋转矩阵并非是点集的正确转换,只是OBB的正确表示方式。这不影响我们使用其OBB作为逻辑包围盒。 TIP:这里引申出一个问题,既然协方差矩阵求特征向量的时候,可以带反射,也可以不带,只是方向不同。那么是否存在不带反射的特征向量的解,笔者线代水平有限就不深入探讨了。 实现代码 import math from numpy import ndarray, dot, cov, transpose, array, min as npmin, max as npmax from numpy.linalg import eigh, det class OBB: def __init__(self): self._rotate_matrix = None # 线性变换矩阵 self._center = None # 中心点 self._extents = None # 宽高长 def transform(self, point): # 点转换到目标 target = dot(array(point) - self._center, self._rotate_matrix) + self._center return self._to_float_list(target) def transform_to_origin(self, point): # 点转换到原始 target = dot(array(point) - self._center, transpose(self._rotate_matrix)) return self._to_float_list(target) def _to_float_list(self, obj_array): return [float(x) for x in obj_array] @property def center(self): return self._to_float_list(self._center) @property def extents(self): return self._to_float_list(self._extents) @property def pitch_yaw_roll(self): R = self._rotate_matrix # 这里是左手系Y-X-Z顺规,其他方式欧拉角请自己计算 sy = math.sqrt(R[2][0] * R[2][0] + R[2][2] * R[2][2]) pitch = math.atan2(-R[2][1], sy) yaw = math.atan2(R[2][0], R[2][2]) if sy > 1e-6 else math.atan2(-R[0][2], R[0][0]) roll = math.atan2(R[0][1], R[1][1]) if sy > 1e-6 else 0 if det(self._rotate_matrix) < 0: # 针对反射矩阵进行特判 roll = -roll return (pitch, yaw, roll) @classmethod def build_from_points(cls, points): if not isinstance(points, ndarray): points = array(points, dtype=float) assert points.shape[1] == 3, 'points have to have 3-elements' covariance_matrix = cov(points, y=None, rowvar=0, bias=1) # 计算协方差矩阵 _, eigen_vectors = eigh(covariance_matrix) # 计算协方差矩阵的特征值和特征矩阵 trans_matrix = eigen_vectors rotate_matrix = transpose(trans_matrix) # 由原始点转换到AABB,求中心和长宽高 p_primes = array([dot(p, trans_matrix) for p in points]) min_p = npmin(p_primes, axis=0) max_p = npmax(p_primes, axis=0) center = dot((min_p + max_p) / 2.0, rotate_matrix) extents = (max_p - min_p) obb = OBB() obb._rotate_matrix = rotate_matrix obb._center = center obb._extents = extents return obb |
【本文地址】
今日新闻 |
推荐新闻 |









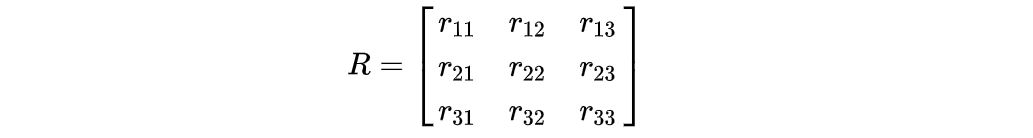
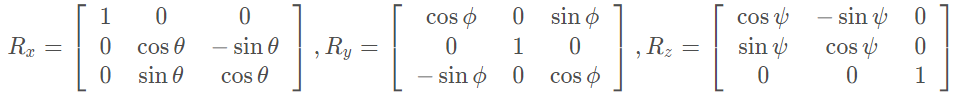
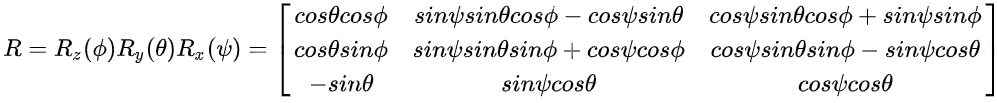

![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jJOM2wre-1646224673429)(http://pfp.ps.netease.com/kmpvt/file/6046df9c6158bc9130027eeezPCud8Gi01?sign=rILqosKG3_DSMkI7evlQZCV19gY=&expire=1646240880)]](https://img-blog.csdnimg.cn/5ed6501a78a64e139719ec9b875c2167.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAd293bzFndA==,size_20,color_FFFFFF,t_70,g_se,x_16)

