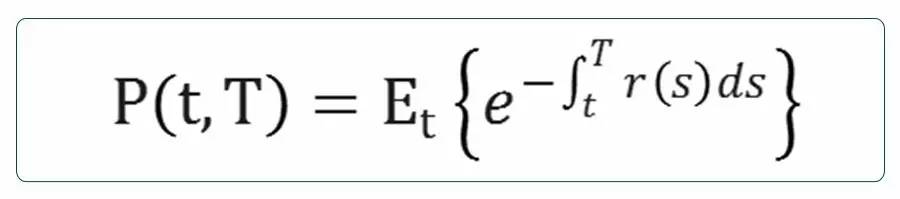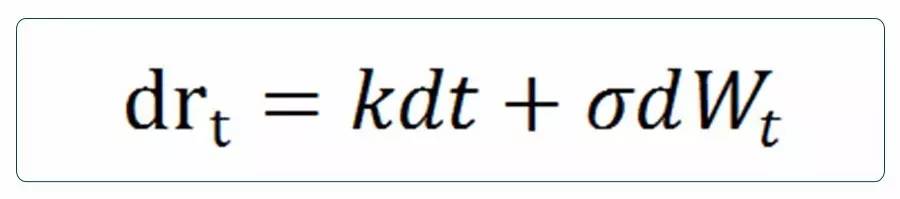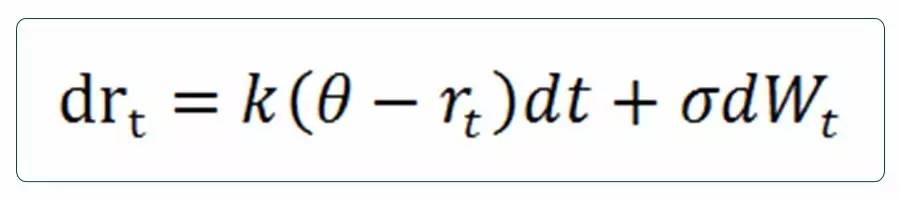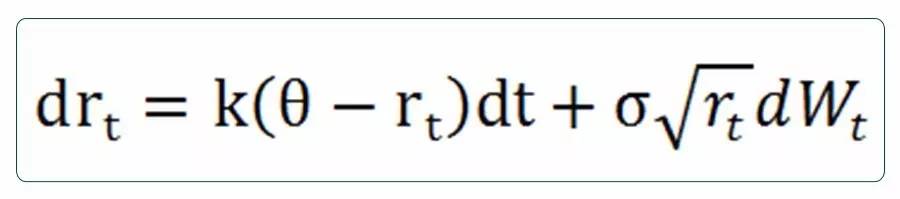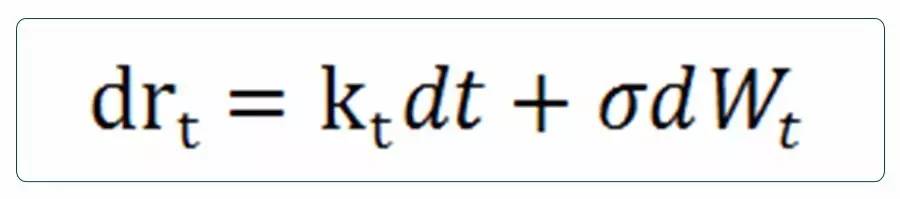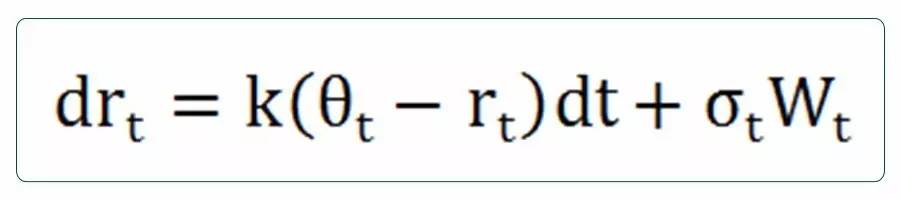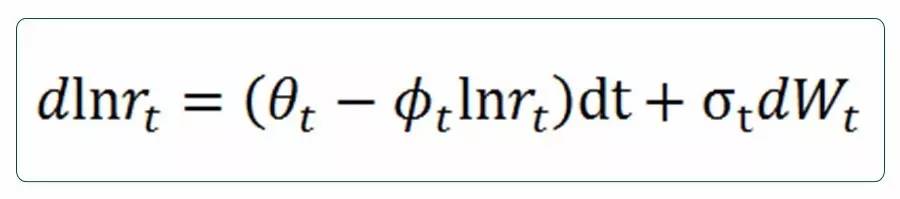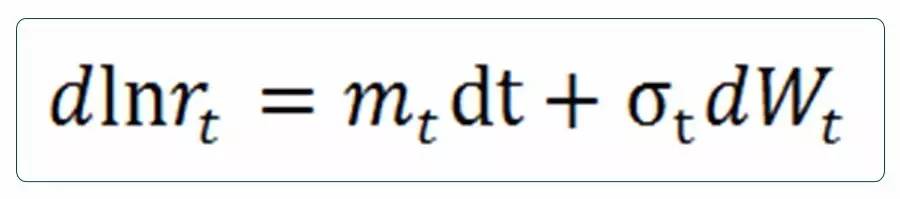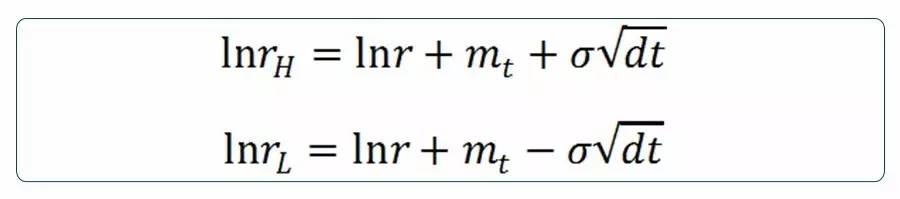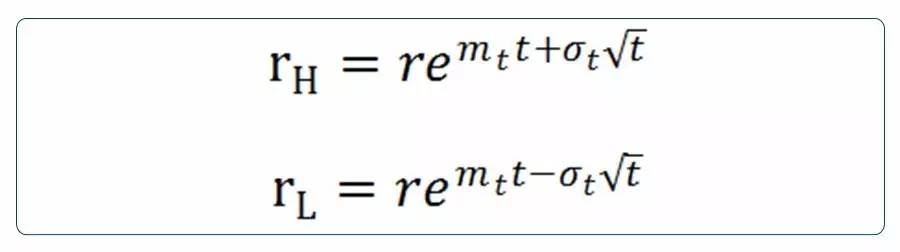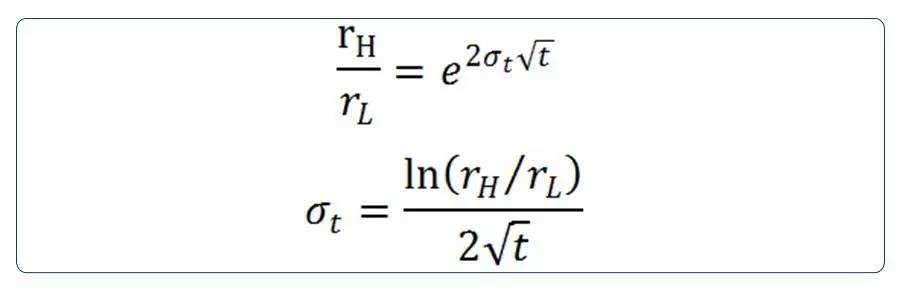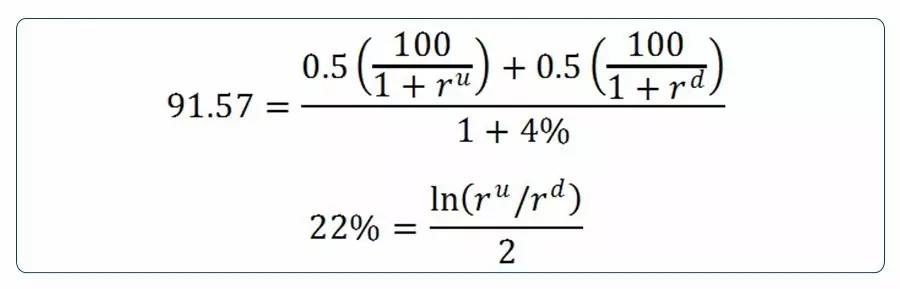其中，表示瞬时利率，R(t,T)表示[t,T]的即期利率。

那么，在连续时间下，零息债券的价格就可以被表示为：

利率模型分为单因子模型和多因子模型，单因子模型假设债券价格仅受瞬时利率这一单一因子的影响。本文仅对单因子模型做出介绍，单因子模型又分为均衡模型和无套利模型。

均衡模型通过将市场中风险偏好、投资机会、风险价格等因素，以参数的形式引入方程，构建利率曲线。由于均衡模型是基于自身假设先确定参数，再构建利率模型，因此，均衡模型的参数具有稳定性，不会随市场期限结构的变动而变动，但是其估计参数的资料更难以获得，构建出的利率模型不能完全的符合市场利率期限结构，难以在实际定价中得到应用。

均衡模型包括：Merton模型、Vasicek模型以及CIR模型等。

（1）Merton模型（1973）

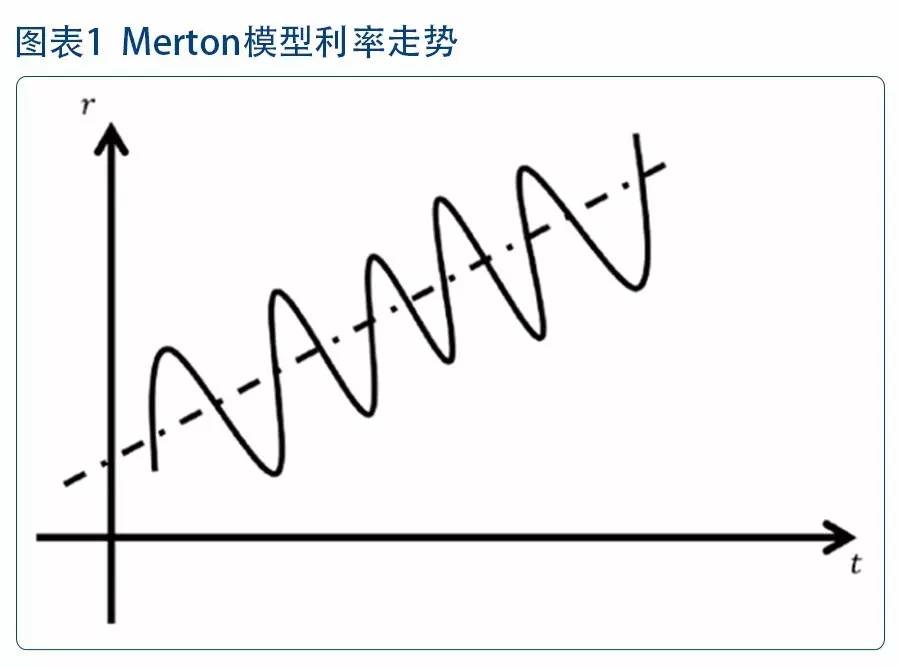
其中，k为漂移项，σ表示瞬时利率的波动率，为布朗运动。

Merton最早提出利率模型，其模型形式最为简单。在Merton模型中，利率由两部分组成：一个确定的部分（漂移项k），以及一个随机的部分（波动项σ）。

由于布朗运动服从正态分布，通过模型得到的利率也服从正态分布，但是值可能会小于0，与实际情况不符。同时，模型没有均值回归的特性，其构建的利率期限结构形态也较为单一。

（2）Vasicek模型（1977）

其中，k表示均值回归调整速度，θ表示瞬时利率平均值（也可视为长期均衡利率），σ表示瞬时利率的波动率，均为正常数。

Vasicek模型通过在漂移项中引入了瞬时利率平均值，使得模型具有了均值回归的特性，同时，模型也可以反映利率期限结构的多种形态。但模型中，利率仍服从正态分布，并未解决利率可能为负的问题。

（3）Cox，Ingersoll & Ross模型（1985）

其中，k，θ，σ均为正常数，2kθ>。

CIR模型假设瞬时利率的波动率与瞬时利率平方根大小成正比，即利率增加时，利率的波动率也会随之增加。通过这一假设，CIR模型的利率服从非中心卡方分布，当2kθ>时，保证了利率恒大于0。同时，CIR模型保留了Vasicek模型中均值回归的特性。因此，CIR模型一经推出便被广泛应用。

但正如在这一节开头提到的，CIR模型也是均衡模型的一种，先得到参数，再构建利率期限结构，所得的期限结构不能与市场完全一致，不适合应用于实际定价。

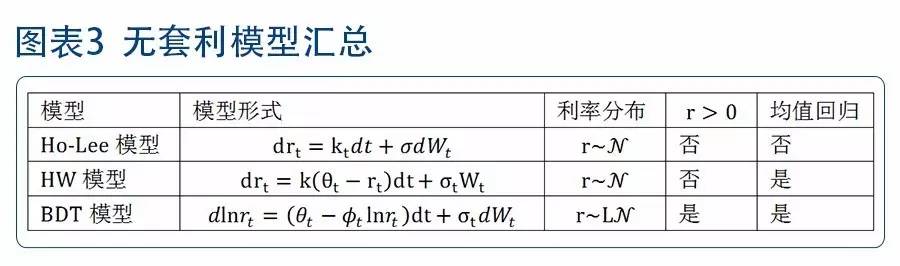
不同于均衡模型，无套利模型通过将利率期限结构作为变量输入模型中，解得参数，再通过二叉树、蒙特卡洛等形式模拟利率期限结构的动态变化。因此，无套利模型得到的利率期限结构能够完全拟合市场曲线。当市场环境发生改变时，模型可以通过调整参数来适应市场实际数据，虽然相比于均衡模型其参数稳定性差，但是更加贴近实际市场实际情况，在资产定价中的商业价值更大。无套利模型包括Ho-Lee模型，Hull White模型，以及BDT模型等。

（1）Ho-Lee模型（1986）

其中，为漂移项系数，为一个随时间变化的变量，σ为瞬时利率波动率，为一个常数。

Ho-Lee模型首次将漂移项系数设置成关于时间的变量，从而使得模型能较好地拟合现实世界的利率曲线，其缺陷是利率服从正态分布，可能为负值，且没有均值回归的特性，并且假设利率的波动率不变，没有考虑利率的波动率结构。

（2）Hull White模型（1990）

其中，k为常数，、为时间变量。

Hull White对模型进行了改进，通过引入参数，使得在完全拟合期限结构之外，还具有均值回归特性。引入参数使得模型能进一步完全拟合波动率期限结构，但利率仍可能为负值。

（3）BDT模型（1990）

其中，、、为时间变量。

BDT模型假设利率服从对数正态分布，保证了其利率恒大于0。

在实际应用中，我们认为，BDT模型能够保证利率恒为正值，符合现实中利率的。同时，BDT也能够保证其拟合出的利率结构与市场一致。因此，综合上述6个模型，我们选择BDT模型对利率路径进行模拟。

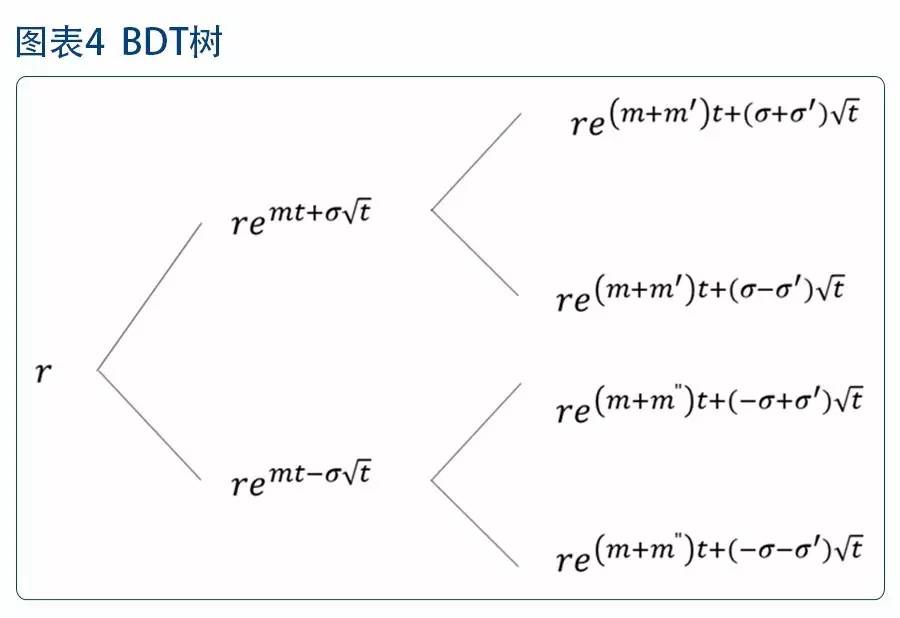
将BDT模型简化写为：

那么，构建二叉树，对于任一时点上的利率r，可得其下一时点

即，

据此，我们可以得到BDT模型的利率二叉树结构如下：

由于波动率随时间变化而变化，可能出现非结合的树图结构（如）。为避免这一情况，模型允许在同一时点，利率上升与下降漂移项不同，即，取m'，m"，使得。

将(12)(13)式相除，我们可以得到波动率的公式：

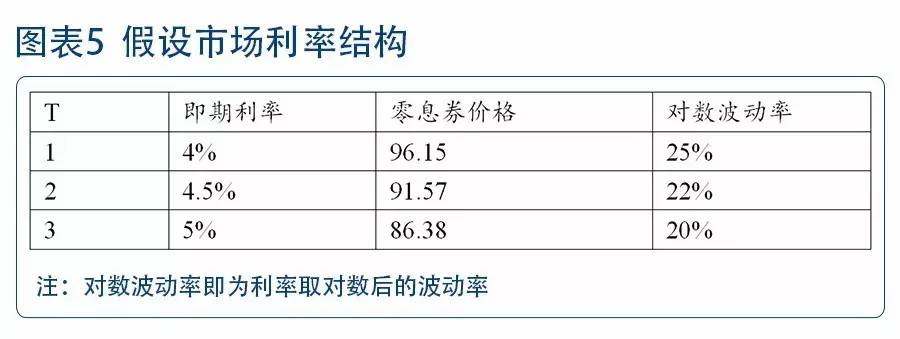
我们用一个例子来说明如何通过实际市场期限结构，构建BDT树。假设当前市场期限结构如下：

那么在这一例中，

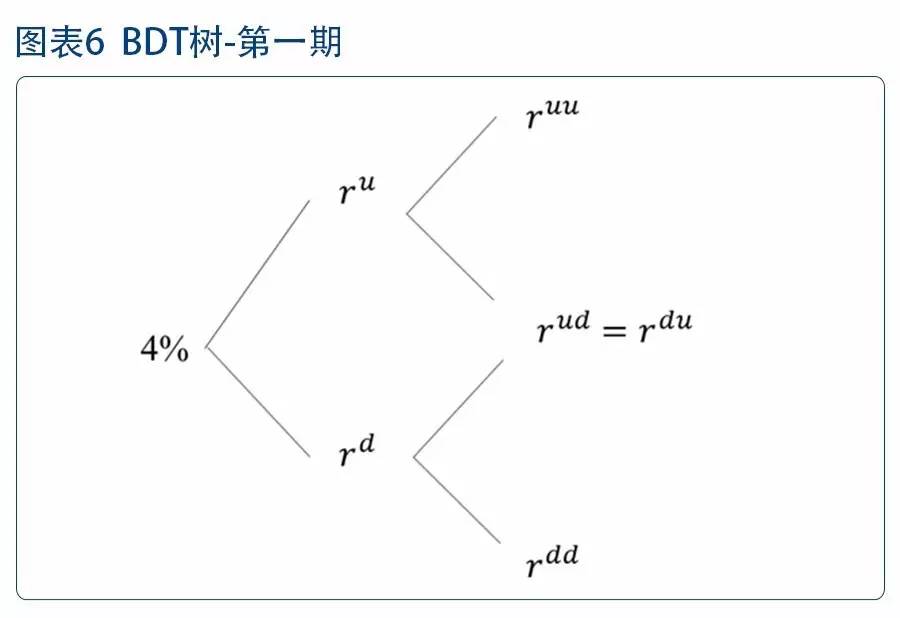
第二年的远期利率价格需要满足：

1、2年期零息债券价格为91.57.

2、对数波动率为22%

即，

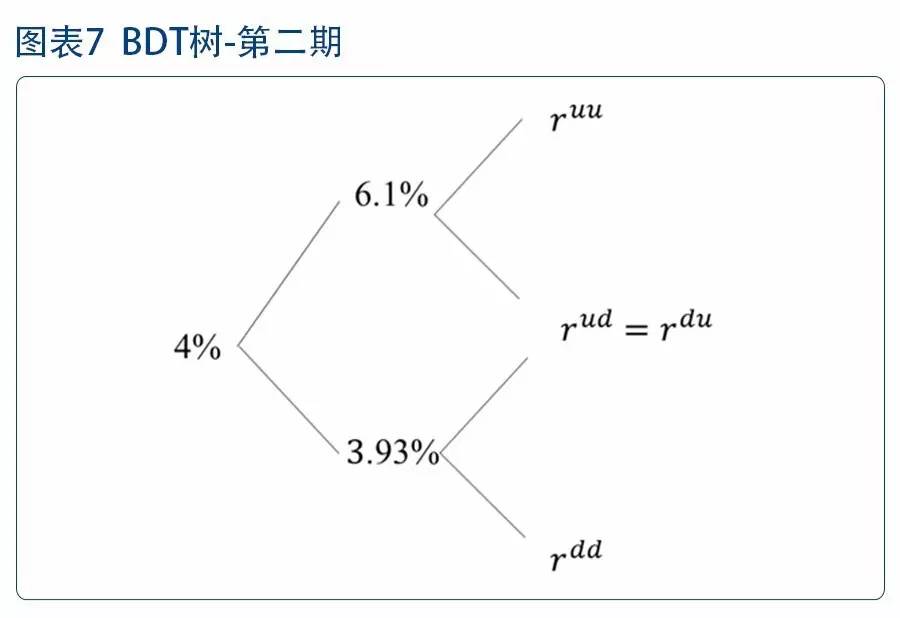
解得=6.1%，=3.93%。接着构建T=3时的利率树。

同样，通过零息债券价格和波动率，第三年的远期利率价格可以由以下等式解出：

可以解得，=8.44%，=5.84%，=4.05%

因此，在该例中，树的结构即为：

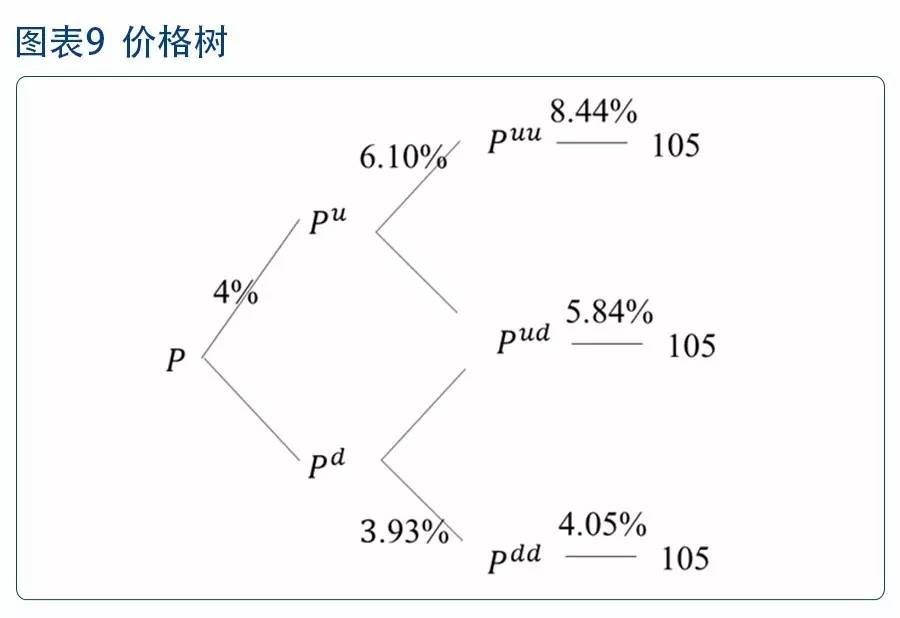
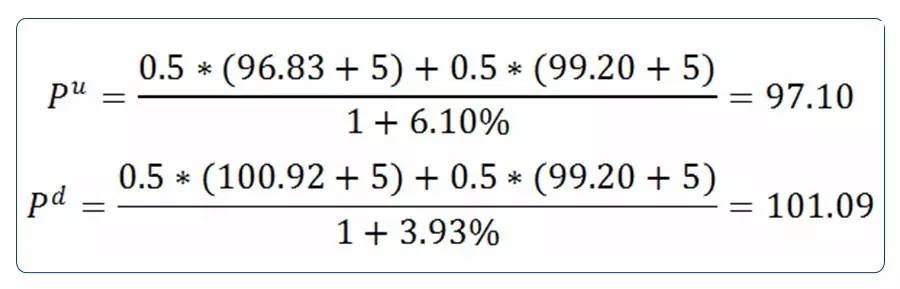
继续沿用上一节的利率结构举例，假设市场中有一只债券，其面值为100，票面利率为5%，期限为3年，每年付息一次，在第1年投资人享有回售权。那么，

（1）现金流折现计算含权债价格

由于，