神经网络结构:生成式对抗网络(GAN) |
您所在的位置:网站首页 › gan算法作者 › 神经网络结构:生成式对抗网络(GAN) |
神经网络结构:生成式对抗网络(GAN)
|
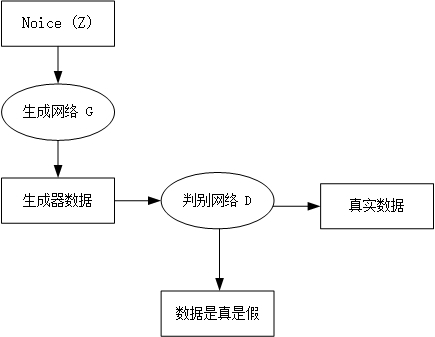
生成对抗网络(GAN),是深度学习模型之一,2014年lan Goodfellow的开篇之作Generative Adversarial Network,GAN是一种无监督学习方法,它巧妙地利用“对抗”的思想来学习生成式模型,一旦训练完成后可以生成全新的数据样本。DCGAN将GAN的概念扩展到卷积神经网络中,可以生成质量较高的图片样本 GAN概述GAN包括两个模型,一个是生成模型 G(Generator),一个是判别模型 D(Discriminator)。他们分别的功能是: G负责生成图片,他接收一个随机的噪声z,通过该噪声生成图片,将生成的图片记为G(z) D负责判别一张图片是不是“真实的”。它的输入是$x$,$x$代表一张图片,输出D(x)表示x为真实图片的概率,如果为1,代表是真实图片的概率为100%,而输出为0,代表不可能是真实的图片(真实实例来源于数据集,伪造实例来源于生成模型)在训练过程中,生成模型G的目标是尽量生成看起来真的和原始数据相似的图片去欺骗判别模型D。而判别模型D的目标是尽量把生成模型G生成的图片和真实的图片区分开来。这样,生成器试图欺骗判别器,判别器则努力不被生成器欺骗。两个模型经过交替优化训练,互相提升,G和D构成了一个动态的“博弈”,这是GAN的基本思想。 最后博弈的结果是什么?在最理想的状态下,G可以生成足以“以假乱真”的图片G(z)。对于D来说,它难以判定G生成的图片究竟是不是真实的,因此D(G(z))=0.5。此时得到了一个生成式的模型G,它可以用来生成图片。 图1-1 GAN网络整体示意图 如上图所示,我们有两个网络,生成网络G(Generayor)和判别网络D(Discriminator)。生成网络接收一个(符合简单分布如高斯分布或者均匀分布的)随机噪声输入,通过这个噪声输出图片,记做G(z)。判别网络的输入是x,x代表一张图片,输出D(x)代表x为真实图片的概率。 GAN模型优化训练目的:将一个随机高斯噪声$z$通过一个生成网络G得到一个和真实数据分布$p_{data}(x)$差不多的生成数据分布$p_G(x;\theta )$,其中$\theta $是网络参数,我们希望找到$\theta $使得$p_G(x;\theta )$和$p_{data}(x)$尽可能的接近。 我们站在判别网络的角度想问题,首先判别器要能识别真实数据,同样也能识别出生成数据,在数学式子上的表达为D(x)=1和D(G(z))=0。我们通过这两个式子,分别来构造[正类](判别出x属于真实数据)和[负类](判别出G(z)属于生成数据)的对数损失函数。 生成网络G的损失函数为$\log (1 - D(G(z)))$或者$ - \log D(G(z))$。 判别网络D的损失函数为$ - (\log D(x) + \log (1 - D(G(z))))$。 我们从式子中解释对抗,损失函数的图像是一个类似于y=log(x)函数图形,x0,x=1时,y=0,生成网络和判别网络对抗(训练)的目的是使得各自的损失函数最小,,生成网络G的训练希望$D(G(z))$趋近于1,也就是正类,这样生成网络G的损失函数$\log (1 - D(G(z)))$就会最小。而判别网络的训练就是一个2分类,目的是让真实数据x的判别概率D趋近于1,而生成数据G(z)的判别概率$D(G(z))$趋近于0,这是负类。 当判别网络遇到真实数据时:${E_{x \sim {p_{data}}(x)}}[\log D(x)]$,这个期望要取最大,只有当D(x)=1的时候,也就是判别网络判别出真实数据是真的。 当判别网络遇到生成数据时:${E_{z \sim Pz(z)}}[\log (1 - D(G(z)))]$,因为0Scott Rome对原论文的推导有这么一个观念,他认为原论文忽略了可逆条件,原论文的推理过程不够完美。我们开看看到底哪里不完美: 在GAN原论文中,有一个思想和其他方法不同,即生成器G不需要满足可逆条件,即G不可逆 scott Rome认为:在实践过程中G就是不可逆的。 其他人:证明时使用积分换元公式,,而积分换元公式恰恰是基于G的可逆条件。 Scott认为证明只能基于以下等式成立: $${E_{z \sim Pz(z)}}[\log (1 - D(G(z)))] = {E_{x \sim {P_G}(x)}}[\log (1 - D(x)]$$ 该等式来源于测度论中的 Radon-Nikodym 定理,它展示在原论文的命题 1 中,并且表达为以下等式: $$\int\limits_x {{p_{data}}(x)} \log D(x)dx + \int\limits_z {p(z)} \log (1 - D(G(z)))dz$$ $$ = \int\limits_x {{p_{data}}(x)} \log D(x)dx + {p_G}(x)\log (1 - D(x))dx$$ 我们这里使用了积分换元公式,但进行积分换元就必须计算 G^(-1),而 G 的逆却并没有假定为存在。并且在神经网络的实践中,它也并不存在。可能这个方法在机器学习和统计学文献中太常见了,因此很多人忽略了它。 满足Radon-Nikodym 定理条件之后。我们利用积分换元变换一下之前定义的目标函数: $$\mathop {\min }\limits_G \mathop {\max }\limits_D V(D,G) = {E_{x \sim {p_{data}}(x)}}[\log D(x)] + {E_{x \sim PG}}[\log (1 - D(x))]$$ 然后通过下面的式子求最优的生成网络模型$${G^*} = \arg \mathop {\min }\limits_G \mathop {\max }\limits_D V(G,D)$$ 最优判别器首先我们只考虑$\mathop {\max }\limits_D V(G,D)$,在给定G的情况下,求一个合适的D使得V(G,D)取得最大。这是一个简单的微积分。 $$\begin{array}{l}V = Ex \sim {P_{data}}[logD(X)] + Ex \sim {P_G}[log(1 - D(x))]\\ = \mathop \smallint \limits_x {P_{data}}(x)\log D(x)dx + \mathop \smallint \limits_x {p_G}(x)\log (1 - D(x))dx\\ = \int_x {[{P_{data}}(x)logD(X)] + {P_G}(x)log(1 - D(x))]dx} \end{array}$$ 对于这个积分,要取其最大值,只要被积函数是最大的,就能求到最大值,我们称之为最优的判别器${D^*}$$${D^*} = {P_{data}}(x)\log D(x) + {P_G}(x)\log (1 - D(x))$$ 在真实数据给定和生成数据给定的前提下,${P_{data}}(x)$和${P_G}(x)$都可以看做是常数,我们用a、b来表示他们,如此一来得到下面的式子:$$\begin{array}{*{20}{l}}{f(D) = a\log (D) + b\log (1 - D)}\\{\frac{{df(D)}}{{dD}} = a*\frac{1}{D} + b*\frac{1}{{{\rm{1}} - {\rm{D}}}}*( - 1) = 0}\\{a*\frac{1}{{{D^*}}} = b*\frac{1}{{1 - {D^*}}}}\\{ \Leftrightarrow a*(1 - {D^*}) = b*{D^{\rm{*}}}}\\{ \Leftrightarrow {D^{\rm{*}}}(x) = \frac{{{P_{data}}(x)}}{{{P_{data}}(x) + {P_G}(x)}}(while{P_{data}}(x) + {P_G}(x) \ne 0)}\end{array}$$ 如果我们继续对f(D)求二阶导,并把极值点${{D^{\rm{*}}}(x) = \frac{{{P_{data}}(x)}}{{{P_{data}}(x) + {P_G}(x)}}}$代入: $$\frac{{df{{(D)}^2}}}{{{d^2}D}} = - \frac{{{P_{data}}(x)}}{{{{(\frac{{{P_{data}}(x)}}{{{P_{data}}(x) + {P_{\rm{G}}}(x)}})}^2}}} - \frac{{{P_{\rm{G}}}(x)}}{{1 - {{(\frac{{{P_{data}}(x)}}{{{P_{data}}(x) + {P_{\rm{G}}}(x)}})}^2}}} < 0$$ 其中0与${P_{data}}(x)$的差异程度就能够取到G使得这两种分布的差异最小,这样自然就能够生成一个和原分布尽可能接近得分布。 还没有结束,哇!证明好累呀,快结束了那就再坚持一下吧。 我们还要进一步证明有且仅有一个G能够达到这个最小值。 我们来介绍一下JS散度, $$JSD(P\parallel Q) = \frac{1}{2}[D(P\parallel M) + D(Q\parallel M)]$$ $$M = \frac{1}{2}(P + Q)$$ 假设存在两个分布 P 和 Q,且这两个分布的平均分布 M=(P+Q)/2,那么这两个分布之间的 JS 散度为 P 与 M 之间的 KL 散度加上 Q 与 M 之间的 KL 散度再除以 2。这里P为${P_{data}}(x)$,Q为${P_G}(x)$。 JS 散度的取值为 0 到 log2。若两个分布完全没有交集,那么 JS 散度取最大值 log2;若两个分布完全一样,那么 JS 散度取最小值 0。 因此V(G,D)可以根据JS散度的定义改写为:$$V(G,D) = - \log 4 + 2*JSD({P_{data}}(x)|{P_G}(x))$$ 这一散度其实就是Jenson-Shannon距离度量的平方。根据他的属性:当${P_G}(x) = {P_{data}}(x)$时,$JSD({P_{data}}(x)|{P_G}(x))$为0。综上所述,生成分布当前仅当等于真实数据分布式时,我们可以取得最优生成器。 原论文还有额外的证明白表示:给定足够的训练数据和正确的环境,训练过程将收敛到最优 G,我们并不详细讨论这一块。 GAN的优缺点 代码实现我们通过GitHub上的一个DCGAN项目介绍TensorFlow中的DCGAN实现。利用该代码主要去完成两件事情,一是生成MNIST手写数字,二是在自己的数据集上训练。 GAN生成MNIST图像在实际训练中,使用梯度下降法,对D和G交替做优化即可,详细的步骤为: 从已知的噪声分布$p_{z(z)}$中选出一些样本$\{z^{(1)}, z^{(2)},····, z^{(m)}\}$ 从训练数据中选出同样个数的真实图片$\{x^{(1)}, x^{(2)},····, x^{(m)}\}$ 设判别器D的参数为$\theta_d$,求出损失关于参数的梯度$\triangledown \frac{1}{m}\sum_{i=1}^m[ln(D(x^{(i)})+ln(1-D(G(z^{(i)}))))]$,对$\theta_d$更新时加上该梯度 设生成器G的参数为$\theta_g$,求出损失关于参数的梯度$\triangledown \frac{1}{m}\sum_{i=1}^m[ln(1-D(G(z^{(i)}))))]$,对$\theta_g$更新时减去该梯度在上面的步骤中,每对D的参数更新一次,便接着更新一次G的参数。有时还可以对D的参数更新k次后再更新一次G的参数,这些要根据训练的实际情况进行调整。另外,要注意的是,由于D是希望损失越大越好,G是希望损失越小越好,所以它们一个是加上梯度,一个是减去梯度。 当训练完成后,可以从$P_z(z)$随机取出一个噪声,经过G运算后可以生成符合P_{data}(x)的新样本。 DCGAN如果要实现用DCGAN生成MNIST手写数字,直接运行 python main.py --dataset mnist --input_height=28 --output_height=28 --train这一节主要讲使用DCGAN生成卡通人物头像。首先需要准备好图片数据并将它们裁剪到统一大小。我们把数据放在项目根目录下的./data/anime文件夹下, python main.py --input_height 96 --input_width 96 \ --output_height 48 --output_width 48 \ --dataset anime --crop -–train \ --epoch 300 --input_fname_pattern "*.jpg"下面分别是训练1、5、50个epoch之后产生的样本效果
使用已经训练好的模型进行测试的对应命令为: python main.py --input_height 96 --input_width 96 --output_height 48 --output_width 48 --dataset anime --crop 参考资料除了本章所讲的GAN和DCGAN外,还有研究者对原始GAN的损失函数做了改进,改进后的模型可以在某些数据集上获得更稳定的生成效果,相关的论文有:Wasserstein GAN、Least Squares GenerativeAdversarial Networks。 训练GAN的技巧清单 这篇博客以下内容我以后再完善 知乎GAN数学推导 机器之心:GAN推理与实现 Scott Rome GAN 推导:http://srome.github.io//An-Annotated-Proof-of-Generative-Adversarial-Networks-with-Implementation-Notes/ Goodfellow NIPS 2016 Tutorial:https://arxiv.org/abs/1701.00160 李弘毅MLDS17:http://speech.ee.ntu.edu.tw/~tlkagk/courses_MLDS17.html |
【本文地址】