GMM:高斯混合模型原理实现与应用 |
您所在的位置:网站首页 › gamma分布python › GMM:高斯混合模型原理实现与应用 |
GMM:高斯混合模型原理实现与应用
|
一、算法思想 生活生产中存在各种各样数据,如我们的身高数据,设备的振动数据,图像的像素数据等。我们之所以看到身高差异、振动频率幅度差异、图像颜色内容差异是由于不同种类的数据在分布上不同。怎样描述上述数据的分布?高斯混合模型(Gaussian Mixture Model)可以近似任意形状的概率分布。GMM的核心思想:任意形状的概率分布可以通过多个单高斯分布的线性组合进行近似。 二、算法应用1、数据分类:由于观测数据的分布可以由多个单高斯分布进行近似。通过判断观测数据属于哪个单高斯分布,从而对数据进行分类。 2、异常检测:数据的异常检测在金融风控、设备状态监测等场景应用广泛。GMM首先对观测数据进行多高斯分布建模,并通过EM算法估计单高斯分布参数,如果测试数据(在线数据)在隶属的高斯分布中的概率密度值小于阈值,则判定为异常点。 3、图像分割:在医学图像分割中应用广泛,通常用于前景以及不同类别的背景之间的分割,本质上与数据分类相同。 4、图像生成:近期在各大平台上火热的AI绘画,为生成式模型作品。GMM能够用于图像生成关键在于其能够通过不同的高斯分布的线性组合对任意图像分布进行拟合。因此,我们通过GMM求出了图像分布,就可以从图像分布中任意采样生成与原数据相似但不同的图像。 三、算法原理1、什么是数据分布? A. 单一高斯分布 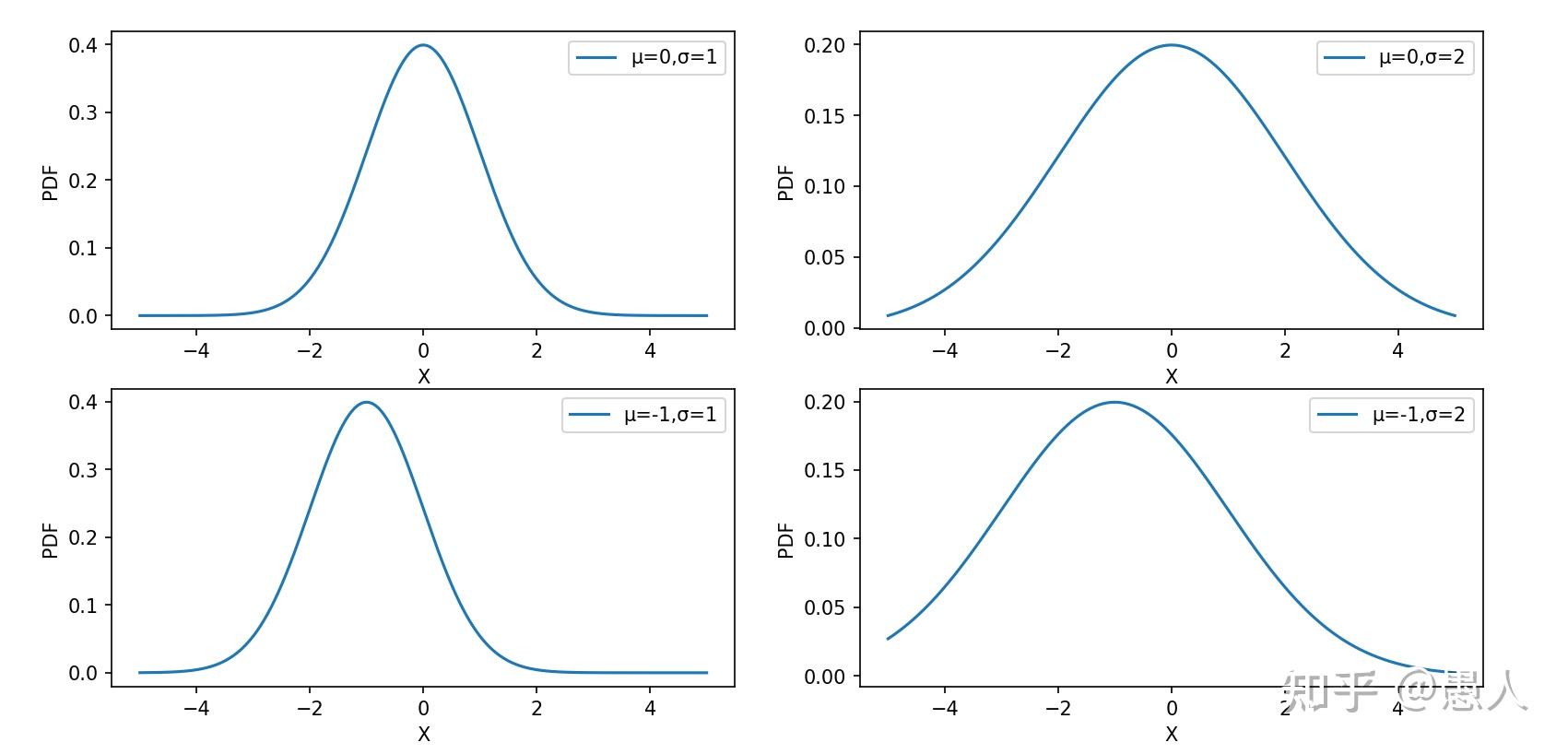 图1. 简单高斯分布(正态分布)曲线 图1. 简单高斯分布(正态分布)曲线图1为简单的高斯分布概率密度曲线,用其描述符合高斯分布的数据,如身高分布等。其概率密度函数如下公式: f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}\ e^{-\frac{(x-\mu)^2}{2\sigma^2}} 由图1可发现如下特征: 高斯概率密度函数呈对称分布;在均值 \mu 处取得最大值;标准差 \sigma 越小,曲线越陡峭,峰值越大,数据分布越集中;概率密度函数所覆盖区域面积为1。B. 混合高斯分布  图2. 混合高斯分布 图2. 混合高斯分布如图2,可以发现,观测数据Data1,Data2,Data3有三个尖峰,单个高斯分布已无法对其进行拟合。如何对该种分布的数据进行拟合?采用高斯混合模型。因为高斯混合模型可通过多个单高斯分布的线性组合近似任意形状的概率分布,上述数据的概率分布也包括在内。  图3. 高斯混合模型数据拟合 图3. 高斯混合模型数据拟合如图3,淡蓝色的直方图为真实数据分布,黑色的曲线为高斯混合模型对于真实数据分布的拟合。k=1,2,3,4,5,6表示采用了k个单高斯分布的线性组合得到了黑色的拟合曲线。可以发现随着个数越多拟合的曲线细节更加丰富,拟合的曲线也更接近真实数据分布。最佳单高斯分布的个数可以通过AIC或BIC指标计算。 2、GMM如何拟合数据分布? 高斯混合模型的概率分布为: P(x|\theta ) = \sum\nolimits_{k = 1}^K {{\alpha _k}} \phi (x|{\theta _k}) 上式表示为高斯混合模型的概率分布为 K 个单高斯分布的线性组合。其中, K 为单高斯分布的个数;{\alpha _k} 为第 k 个高斯分布被选中的概率;\phi (x|{\theta _k}) 为第k个高斯分布的概率密度函数;\theta = ({\mu _k},{\sigma _k},{\alpha _k})问题:给定一组未知分布的数据 X = \{ {x_1},{x_2},...{x_N}\} ,怎样估计高斯混合模型的参数 \theta 来拟合数据分布? 方案:对于数据分布的拟合问题,我们首先想到的是构建最大似然函数然后求解参数,即找到一组最优的参数 \widehat \theta ,使得在该参数下数据的概率密度值最大,即该参数下的概率密度函数最大程度的拟合了数据分布。 因此,我们首先构建似然函数: \log (L(\theta )) = \sum\nolimits_{i = 1}^N {\log (\sum\nolimits_{k = 1}^K {{\alpha _k}} \phi ({x_j}|{\theta _k}))} 我们的目标:从无数的 \theta = ({\mu _k},{\sigma _k},{\alpha _k}) 从挑选最优的 \widehat \theta 来最大化 \log (L(\theta )) 对于数据 \{ {x_1},{x_2},...{x_N}\} 中的每个点,实际上我们并不知道其来自哪个分布,也不知道该分布下的参数 {\mu _k},{\sigma _k} 是多少。怎样进行估计? 这里用到基于迭代思想的EM算法,来估计参数。这里不详细介绍一般性EM算法推导,只介绍其在GMM参数求解中的应用。其核心思想如下: a. 假设每个高斯模型被选中的概率 {\alpha _k} 以及高斯模型的参数 {\mu _k},{\sigma _k} 已知。我们计算每个点来自每个高斯分布的可能性: {\gamma _{jk}} = \frac{{{\alpha _k}\phi ({x_j}|{\theta _k})}}{{\sum\nolimits_{k = 1}^K {{\alpha _k}} \phi ({x_j}|{\theta _k})}},j = 1,2,...N;k = 1,2,...K b. 根据计算出的每个点所属的分布的可能性,以及每个高斯分布的参数,更新新一轮参数 \begin{array}{l} {\mu _k} = \frac{{\sum\nolimits_{j = 1}^N {{\gamma _{jk}}{x_j}} }}{{\sum\nolimits_{j = 1}^N {{\gamma _{jk}}} }},k = 1,2,...,K\\ {\sigma _k} = \frac{{\sum\nolimits_{j = 1}^N {{\gamma _{jk}}({x_j} - {\mu _k}){{({x_j} - {\mu _k})}^T}} }}{{\sum\nolimits_{j = 1}^N {{\gamma _{jk}}} }},k = 1,2,...K\\ {\alpha _k} = \frac{{\sum\nolimits_{j = 1}^N {{\gamma _{jk}}} }}{N},k = 1,2,...,K \end{array} c. 重复计算,a,b两步直至 \left\| {{\theta _{i + 1}} - {\theta _i}} \right\| < \varepsilon 举个简单的例子对上述式子进行说明: 假设有6个未知分布的数据 \{ {x_1},{x_2},...{x_6}\} ,采用2个高斯分布线性组合对其进行拟合。  图4. GMM参数估计 图4. GMM参数估计第一步(E步):由上述的a步可计算出 {x_1} 来自 {k_1,k_2} 分布的概率 {\gamma _{11}},{\gamma _{12}} ,类似的可以计算出其余5个数据来自两个分布的概率; 第二步(M步):更新概率分布1与概率分布2的均值 {\mu _k} 、方差 \sigma _k 以及每个概率分布被选中的概率 \alpha _k ; 第三步:重复计算,以上两步直至 \left\| {{\theta _{i + 1}} - {\theta _i}} \right\| < \varepsilon 下面通过python代码从头实现GMM。 首先,通过python生成一些1D高斯分布数据,数据来自三个不同的高斯分布。 import numpy as np n_samples = 100 mu1, sigma1 = -5, 1.2 mu2, sigma2 = 5, 1.8 mu3, sigma3 = 0, 1.6 x1 = np.random.normal(loc = mu1, scale = np.sqrt(sigma1), size = n_samples) x2 = np.random.normal(loc = mu2, scale = np.sqrt(sigma2), size = n_samples) x3 = np.random.normal(loc = mu3, scale = np.sqrt(sigma3), size = n_samples) X = np.concatenate((x1,x2,x3))并使用如下代码对数据进行可视化 from scipy.stats import norm def plot_pdf(mu,sigma,label,alpha=0.5,linestyle='k--',density=True): """ Plot 1-D data and its PDF curve. """ # Compute the mean and standard deviation of the data # Plot the data X = norm.rvs(mu, sigma, size=1000) plt.hist(X, bins=50, density=density, alpha=alpha,label=label) # Plot the PDF x = np.linspace(X.min(), X.max(), 1000) y = norm.pdf(x, mu, sigma) plt.plot(x, y, linestyle)plot_pdf(mu1,sigma1,label=r"$\mu={} \ ; \ \sigma={}$".format(mu1,sigma1)) plot_pdf(mu2,sigma2,label=r"$\mu={} \ ; \ \sigma={}$".format(mu2,sigma2)) plot_pdf(mu3,sigma3,label=r"$\mu={} \ ; \ \sigma={}$".format(mu3,sigma3)) plt.legend() plt.show() 图5. 原始数据分布 图5. 原始数据分布如图5,黑色曲线为三种数据的概率密度曲线,蓝、绿、黄直方图为从三种概率密度曲线种采样到的数据。 第一步:初始化均值、方差以及权重 def random_init(n_compenents): """Initialize means, weights and variance randomly and plot the initialization """ pi = np.ones((n_compenents)) / n_compenents means = np.random.choice(X, n_compenents) variances = np.random.random_sample(size=n_compenents) plot_pdf(means[0],variances[0],'Random Init 01') plot_pdf(means[1],variances[1],'Random Init 02') plot_pdf(means[2],variances[2],'Random Init 03') plt.legend() plt.show() return means,variances,pi第二步(E步):计算每个点来自不同高斯分布的概率 def step_expectation(X,n_components,means,variances): """E Step Parameters ---------- X : array-like, shape (n_samples,) The data. n_components : int The number of clusters means : array-like, shape (n_components,) The means of each mixture component. variances : array-like, shape (n_components,) The variances of each mixture component. Returns ------- weights : array-like, shape (n_components,n_samples) """ weights = np.zeros((n_components,len(X))) for j in range(n_components): weights[j,:] = norm(loc=means[j],scale=np.sqrt(variances[j])).pdf(X) return weights第三步(M步):更新参数 def step_maximization(X,weights,means,variances,n_compenents,pi): """M Step Parameters ---------- X : array-like, shape (n_samples,) The data. weights : array-like, shape (n_components,n_samples) initilized weights array means : array-like, shape (n_components,) The means of each mixture component. variances : array-like, shape (n_components,) The variances of each mixture component. n_components : int The number of clusters pi: array-like (n_components,) mixture component weights Returns ------- means : array-like, shape (n_components,) The means of each mixture component. variances : array-like, shape (n_components,) The variances of each mixture component. """ r = [] for j in range(n_compenents): r.append((weights[j] * pi[j]) / (np.sum([weights[i] * pi[i] for i in range(n_compenents)], axis=0))) #5th equation above means[j] = np.sum(r[j] * X) / (np.sum(r[j])) #6th equation above variances[j] = np.sum(r[j] * np.square(X - means[j])) / (np.sum(r[j])) #4th equation above pi[j] = np.mean(r[j]) return variances,means,pi第四步:循环第二、三步至收敛 def train_gmm(data,n_compenents=3,n_steps=50, plot_intermediate_steps_flag=True): """ Training step of the GMM model Parameters ---------- data : array-like, shape (n_samples,) The data. n_components : int The number of clusters n_steps: int number of iterations to run """ #intilize model parameters at the start means,variances,pi = random_init(n_compenents) for step in range(n_steps): #perform E step weights = step_expectation(data,n_compenents,means,variances) #perform M step variances,means,pi = step_maximization(X, weights, means, variances, n_compenents, pi) plot_pdf(means,variances)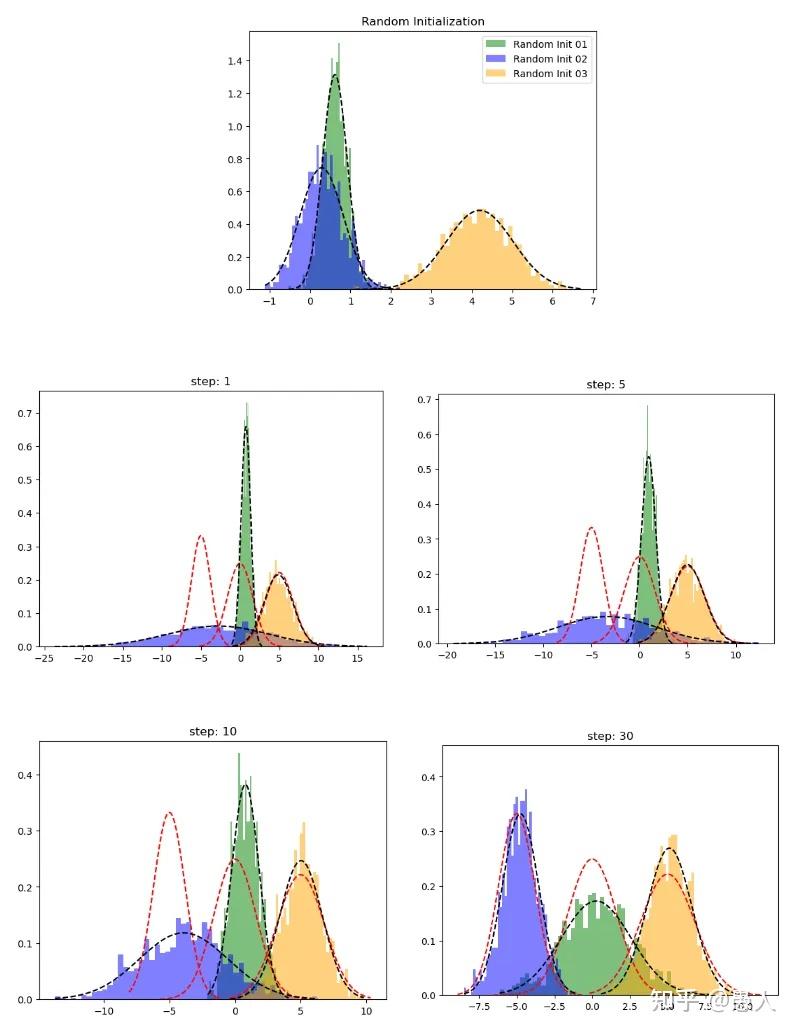 图6. EM算法GMM数据拟合过程 图6. EM算法GMM数据拟合过程在上图中,红色虚线表示原始分布,而其他图表示学习分布。第 30 次迭代后,我们可以看到模型在这个数据集上表现良好。 3、拟合后的数据分布怎样应用? (1)数据聚类 import numpy as np import matplotlib.pyplot as plt from sklearn.mixture import GaussianMixture # 生成随机数据 np.random.seed(0) n_samples = 1000 X = np.random.randn(n_samples, 2) # 创建GMM模型对象并拟合数据 n_clusters = 4 gmm = GaussianMixture(n_components=n_clusters).fit(X) # 预测每个样本所属的聚类 labels = gmm.predict(X) # 可视化聚类结果 plt.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis') plt.show() 图7. GMM数据聚类 图7. GMM数据聚类如上图,我们生成了1000个二维数据。我们采用四个高斯分布进行数据拟合,并判断每个点数据四个高斯分布的概率,并将每个点归为概率最大的高斯分布类别,这样我们将数据分成了四类。 (2)图像生成 我们以手写体数字生成为例,利用GMM拟合图像数据分布,并从拟合后的分布中对数据进行采样,从而生成新的手写体数字。 首先,加载手写体数字数据集,并对图像进行可视化。从60000张数据中选择2000张作为观测数据,通过GMM对2000张数据分布进行拟合。 import numpy as np from sklearn.mixture import GaussianMixture from keras.datasets import mnist import matplotlib.pyplot as plt from sklearn.decomposition import PCA # 加载MNIST数据集 (train_images, train_labels), (test_images, test_labels) = mnist.load_data() train_images_part = train_images[:2000] train_labels_part = train_labels[:2000] # 显示前10张图片 fig, axes = plt.subplots(nrows=2, ncols=5, figsize=(8, 4)) for ax, image, label in zip(axes.ravel(), train_images_part[:10], train_labels_part[:10]): ax.imshow(image, cmap=plt.cm.gray_r) ax.set_xticks([]) ax.set_yticks([]) ax.set_title('Label: {}'.format(label)) plt.tight_layout() plt.show() 图8. 原始图像 图8. 原始图像其次,由于图像为28*28=784维,GMM对高维数据拟合难以收敛,因此,对数据通过PCA进行降维。我们保留85%的主成分,将图像维度降为56维。降维后的图像如图9所示,图像虽部分边缘模糊,但保留了原始图像的主要特征。 train_images_flatten = np.resize(train_images_part, (train_images_part.shape[0], train_images_part.shape[1] * train_images_part.shape[2])) pca = PCA(0.85, whiten=True) data = pca.fit_transform(train_images_flatten) data_rec_flatten = pca.inverse_transform(data) data_rec = np.resize(data_rec_flatten, (train_images_part.shape[0], train_images_part.shape[1], train_images_part.shape[2])) data_rec = np.maximum(data_rec, 0) fig, axes = plt.subplots(nrows=2, ncols=5, figsize=(8, 4)) for ax, image, label in zip(axes.ravel(), data_rec[:10], train_labels_part[:10]): ax.imshow(image, cmap=plt.cm.gray_r) ax.set_xticks([]) ax.set_yticks([]) ax.set_title('Label: {}'.format(label)) plt.tight_layout() plt.show()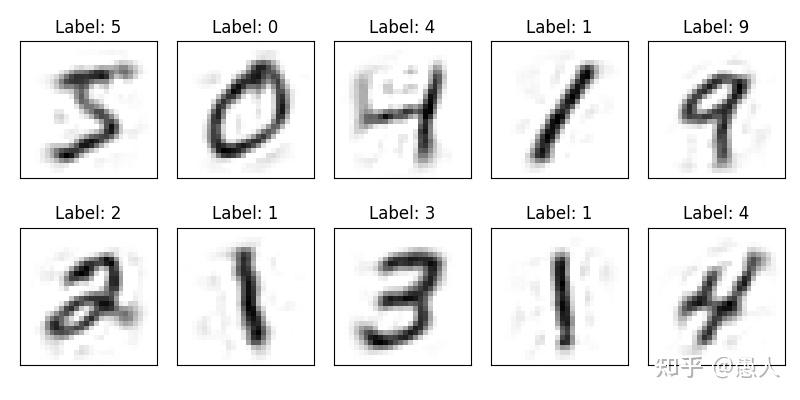 图9. 降维图像 图9. 降维图像最后,我们通过GMM对(2000,56)数据进行拟合,并从中采样10组数据,重建出生成新图像。如图10所示,我们从GMM拟合数据分布中随机采样了10组点,并通过升维重建出了原始图像。可以发现,新生成的图像与原始图像具有较高相似度。 gmm = GaussianMixture(110, covariance_type='full', random_state=2) gmm.fit(data) data_new = gmm.sample(10) digits_new = pca.inverse_transform(data_new[0]) digits_new = np.resize(digits_new, (digits_new.shape[0], train_images_part.shape[1], train_images_part.shape[2])) digits_new = np.maximum(digits_new, 0) fig, axes = plt.subplots(nrows=2, ncols=5, figsize=(8, 4)) for ax, image in zip(axes.ravel(), digits_new[:10]): ax.imshow(image, cmap=plt.cm.gray_r) ax.set_xticks([]) ax.set_yticks([]) plt.tight_layout() plt.show() 图10. 生成图像 图10. 生成图像补充一句:从数据分布中采样是什么意思?如下图,淡蓝色的直方图为1000个观测数据。黑色曲线为gmm拟合的概率密度曲线。紫色、绿色以及红色曲线为三个单高斯概率密度曲线。黑色曲线为三个单高斯曲线的加权。 现在从黑色曲线中采样500个数据,其数据分布为黄色直方图,可以发现黄色直方图与淡蓝色直方图取值以及数据分布基本接近,因此,两者数据分布接近。  图11. gmm采样 图11. gmm采样总结:高斯混合模型是一种重要的数据分布拟合方法。最近大火的AIGC中的图像生成,VAE,DDPM等方法都可以看到GMM的身影。如果我们已知图像的数据分布,我们在数据分布中采样数据就可以生成现实世界中不存在但又与观测样本数据相似的新图像了。可问题是,图像数据分布我们往往难以求解,即我们不知道哪些像素点的组合是来自观测样本数据分布。因此,可以通过高斯混合模型进行逼近,然后从中采样数据,通过解码器等操作生成新图像。 |
【本文地址】
今日新闻 |
推荐新闻 |