MKL库解线性最小二乘问题(LAPACKE |
您所在的位置：网站首页 › fortran求最大值函数 › MKL库解线性最小二乘问题(LAPACKE |
MKL库解线性最小二乘问题(LAPACKE
|
LAPACK（Linear Algebra PACKage）库，是用Fortran语言编写的线性代数计算库，包含线性方程组求解（AX=B）、矩阵分解、矩阵求逆、求矩阵特征值、奇异值等。该库用BLAS库做底层运算。 本示例将使用MKL中的LAPACK库计算线性最小二乘问题的解，首先简单介绍最小二乘法原理： 引用自https://www.cnblogs.com/pinard/p/5976811.html 最小二乘法其形式如下式： \[目标函数=\Sigma(观测值-理论值)^2 \]观测值就是多组样本，理论值就是假设的拟合函数，目标函数也就是在机器学习中常说的损失函数，我们的目标是得到使损失函数最小化时的拟合函数的模型。 以最简单的线性回归为例，比如有\(m\)个样本，表示为\((x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),\dots (x^{(m)},y^{(m)})\)，每个样本都只有一个特征，那么可采用的拟合函数为\(h_{\theta}\left(x\right)=\theta_{0}+\theta_{1} x\)，损失函数为 \[J\left( {{\theta _0},{\theta _1}} \right) = \sum\limits_{i = 1}^m {\left( {{y^{(i)}} - {h_\theta }\left( {{x^{(i)}}} \right)} \right)} = \sum\limits_{i = 1}^m {{{\left( {{y^{(i)}} - {\theta _0} - {\theta _1}{x^{(i)}}} \right)}^2}} \]要使损失函数最小化，仅需去求满足\(\frac{\partial}{\partial \theta_0} J(\theta_0,\theta_1)=0,\frac{\partial}{\partial \theta_1} J(\theta_0,\theta_1)=0,\dots\)时的\(\theta_j\)即可。 接下来来到矩阵法求解： 假设函数\(h_{\theta}\left(x_{1}, x_{2}, \ldots x_{n}\right)=\theta_{0}+\theta_{1} x_{1}+\ldots+\theta_{n-1} x_{n-1}\)，为\(m \times 1\)的向量，其矩阵表达形式为： \[h_{\theta}\left(x\right)=\boldsymbol {X}\theta \]其中\(\theta\)为\(n \times 1\)的向量，\(\boldsymbol{X}\)为\(m \times n\)维的矩阵，其中\(m\)代表样本数，\(n\)代表特征数。则损失函数定义为： \[J(\theta ) = \frac{1}{2}{({\boldsymbol{X}}\theta - {\boldsymbol{Y}})^T}({\boldsymbol{X}}\theta - {\boldsymbol{Y}}) \]根据最小二乘法原理，损失函数对\(\theta\)求导，结果为： \[\frac{\partial}{\partial \theta} J(\theta)=\boldsymbol{X}^{T}(\boldsymbol{X} \theta-\boldsymbol{Y})=0 \]整理后得到 \[\theta=\left(\boldsymbol{X}^{T} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{T} \boldsymbol{Y} \]即只要有输入数据，无需求导也可完成对系数\(\theta\)的求解。 QR分解 实数矩阵的\(QR\)分解就是把矩阵\(A\)分解为一个正交矩阵\(Q\)和一个上三角矩阵\(R\)：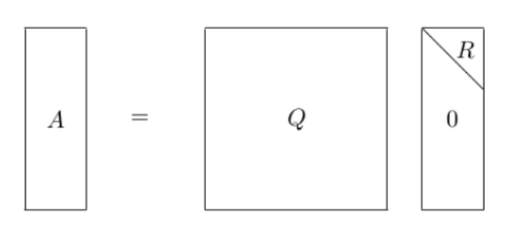 
即\(A=QR\)，其中\(QQ^T=I\)。回到求解最小二乘的最优解\(\theta^*\)： \[\begin{array}{l} {\theta ^*} = {\left( {{{\bf{X}}^T}{\bf{X}}} \right)^{ - 1}}{{\bf{X}}^T}{\bf{Y}}\\ \Rightarrow {\left( {{{\bf{X}}^T}{\bf{X}}} \right)^{ - 1}}{\theta ^*} = {{\bf{X}}^T}{\bf{Y}}\\ \Rightarrow \left( {{{(QR)}^T}QR} \right){\theta ^*} = {(QR)^T}{\bf{Y}}\\ \Rightarrow \left( {{R^T}{Q^T}QR} \right){\theta ^*} = {R^T}{Q^T}{\bf{Y}}\\ \Rightarrow {R^T}R{\theta ^*} = {R^T}{Q^T}{\bf{Y}}\\ \Rightarrow R{\theta ^*} = {Q^T}{\bf{Y}}\\ \Rightarrow {\theta ^*} = {R^{ - 1}}{Q^T}{\bf{Y}} \end{array} \]其中\(R\)为上三角矩阵，求逆相对容易，从而规避了直接对\({\left( {{{\bf{X}}^T}{\bf{X}}} \right)^{ - 1}}\)求逆的高复杂度问题。 MKL的LAPACK库中LAPACKE_?gels，采用\(QR\)分解完成最小二乘法求解这一过程。 1 参数详解 lapack_int LAPACKE_dgels( matrix_layout, // 矩阵布局，行优先或列优先 trans, // 指定矩阵A的计算形式。"N":A,"T":A转置,"C":A共轭转置 m, // 矩阵A的行 n, // 矩阵A的列 nrhs, // 矩阵B的列 a, // 矩阵A，在最小二乘问题中即为X矩阵 lda, // A矩阵的第一维 b, // 矩阵B，在最小二乘问题中即为Y矩阵 ldb ); // B矩阵的第一维 2 定义∥Xθ-Y∥ #include #include #include "mkl_lapacke.h" // 参数 #define M 6 #define N 4 #define NRHS 2 #define LDA N #define LDB NRHS MKL_INT m = M, n = N, nrhs = NRHS, lda = LDA, ldb = LDB, info; double X[LDA*M] = { // X矩阵 1.44, -7.84, -4.39, 4.53, -9.96, -0.28, -3.24, 3.83, -7.55, 3.24, 6.27, -6.64, 8.34, 8.09, 5.28, 2.06, 7.08, 2.52, 0.74, -2.47, -5.45, -5.70, -1.19, 4.70 }; double y[LDB*M] = { // y矩阵 8.58, 9.35, 8.26, -4.43, 8.48, -0.70, -5.28, -0.26, 5.72, -7.36, 8.93, -2.52 }; 3 执行求解 LAPACKE_dgels(LAPACK_ROW_MAJOR, 'N', m, n, nrhs, X, lda, y, ldb)输出为：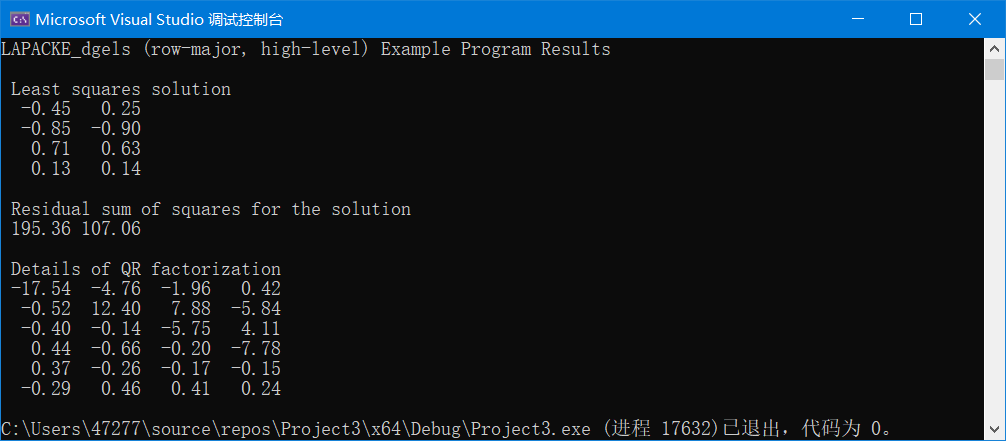 
完整代码
#include
#include
#include "mkl_lapacke.h"
//展示矩阵和向量
extern void print_matrix(const char* desc, MKL_INT m, MKL_INT n, double* a, MKL_INT lda);
extern void print_vector_norm(const char* desc, MKL_INT m, MKL_INT n, double* a, MKL_INT lda);
#define M 6
#define N 4
#define NRHS 2
#define LDA N
#define LDB NRHS
int main() {
/* Locals */
MKL_INT m = M, n = N, nrhs = NRHS, lda = LDA, ldb = LDB, info;
/* Local arrays */
double X[LDA * M] = {
1.44, -7.84, -4.39, 4.53,
-9.96, -0.28, -3.24, 3.83,
-7.55, 3.24, 6.27, -6.64,
8.34, 8.09, 5.28, 2.06,
7.08, 2.52, 0.74, -2.47,
-5.45, -5.70, -1.19, 4.70
};
double y[LDB * M] = {
8.58, 9.35,
8.26, -4.43,
8.48, -0.70,
-5.28, -0.26,
5.72, -7.36,
8.93, -2.52
};
printf("LAPACKE_dgels (row-major, high-level) Example Program Results\n");
// 求解最小二乘
info = LAPACKE_dgels(LAPACK_ROW_MAJOR, 'N', m, n, nrhs, X, lda, y, ldb);
// 检查收敛
if (info > 0) {
printf("The diagonal element %i of the triangular factor ", info);
printf("of A is zero, so that A does not have full rank;\n");
printf("the least squares solution could not be computed.\n");
exit(1);
}
// 打印
print_matrix("Least squares solution", n, nrhs, y, ldb);
print_vector_norm("Residual sum of squares for the solution", m - n, nrhs,
&y[n * ldb], ldb);
print_matrix("Details of QR factorization", m, n, X, lda);
exit(0);
}
// 展示矩阵、向量
void print_matrix(const char* desc, MKL_INT m, MKL_INT n, double* a, MKL_INT lda) {
MKL_INT i, j;
printf("\n %s\n", desc);
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) printf(" %6.2f", a[i * lda + j]);
printf("\n");
}
}
void print_vector_norm(const char* desc, MKL_INT m, MKL_INT n, double* a, MKL_INT lda) {
MKL_INT i, j;
double norm;
printf("\n %s\n", desc);
for (j = 0; j < n; j++) {
norm = 0.0;
for (i = 0; i < m; i++) norm += a[i * lda + j] * a[i * lda + j];
printf(" %6.2f", norm);
}
printf("\n");
}
|
【本文地址】
今日新闻 |
推荐新闻 |