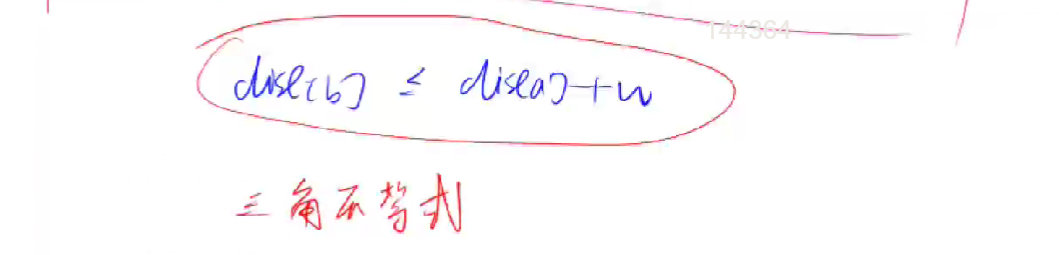【算法基础】 Acwing 图论 之 最短路 (Dijkstra |
您所在的位置：网站首页 › ford算法求最短路 › 【算法基础】 Acwing 图论 之 最短路 (Dijkstra |
【算法基础】 Acwing 图论 之 最短路 (Dijkstra
|
迪杰斯特拉算法适用于求正权有向图中，源点到其余各个节点的最短路径。注意：图中可以有环或重边，但不能有负权边。 求一号点到其他所有点的最短距离 朴素版Dijksatra【稠密图】O(n2)题目链接 思路 【基于贪心】 图的存储 ：邻接矩阵首先 初始化：dist[1] = 0 dist[other] = INF st[i]:记录是否找到了源点到该节点的最短距离然后：循环n次【每次可以确定一个点到起点的最短路】 1、每次的第一步：找到当前没有确定最短路长度的点当中距离最小的那一个 . 2、然后把该点加入到集合 3、用t 更新 1 -> j 路径的长度 (下图)
C++ 代码 【适用于稠密图】
#include
using namespace std;
const int N = 510;
int n,m;
int g[N][N];//图
int dist[N];//距离
bool st[N];
int dijkstra() {
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i
//如果当前点没有确定最短路且 没有更新 or t不是最短的
if(!st[j] && (t == -1 || dist[t] > dist[j])) {
t = j;//更新
}
}
st[t] = true;//把t加到集合里面
for (int j = 1; j
return -1;
}
return dist[n];
}
int main () {
scanf("%d%d", &n, &m);
memset(g, 0x3f, sizeof g);
while (m --) {
int a,b,c;
scanf("%d%d%d", &a, &b, &c);
g[a][b] = min(g[a][b],c);
}
int t = dijkstra();
printf("%d\n" , t);
return 0;
}
Dijkstra 【稀疏图】O(m*log n)
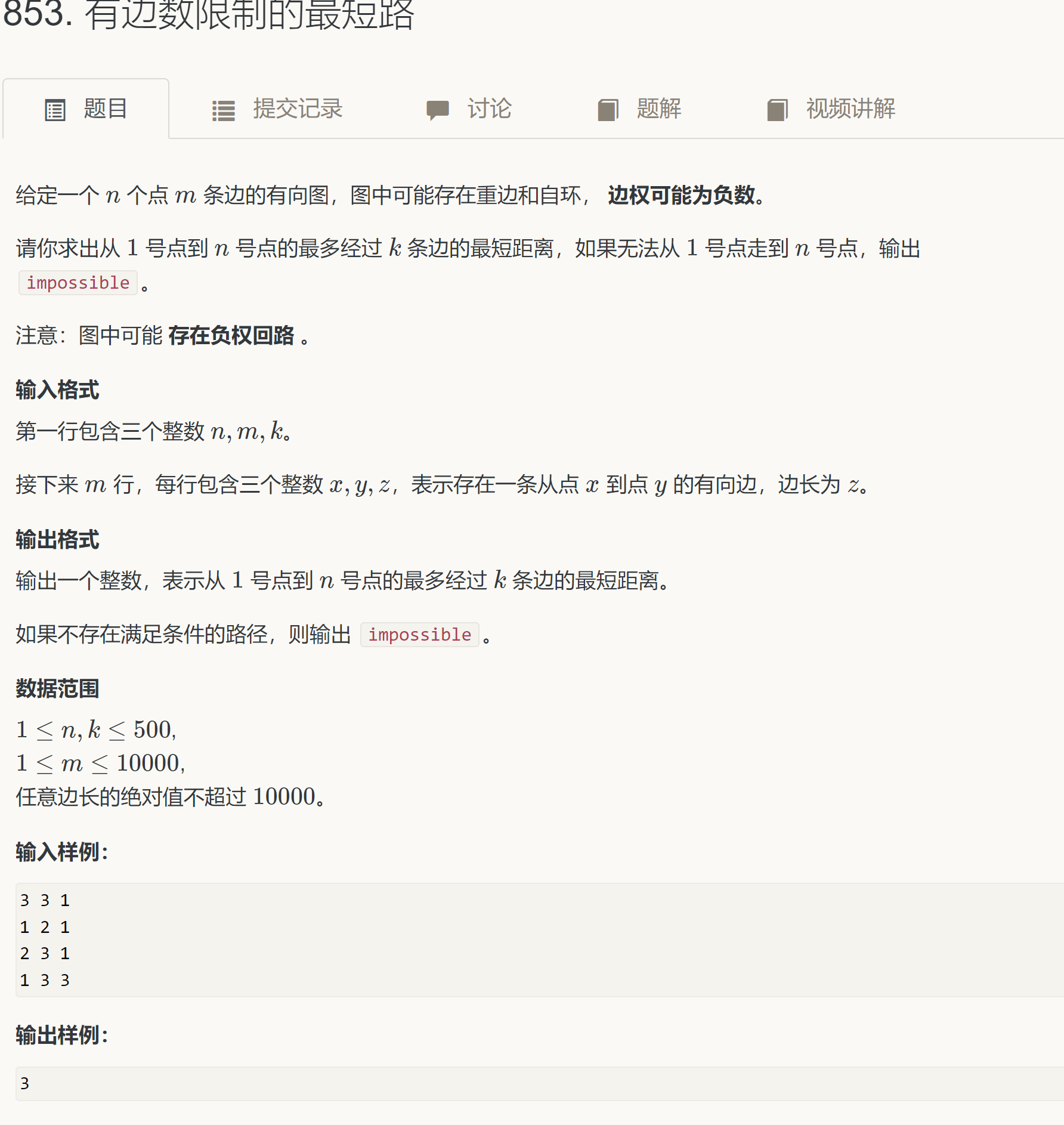
适用于稀疏图 稀疏图是遍历从t出去的所以边，而稠密图是每条边都遍历了 #include #include #include #include //堆的头文件 using namespace std; typedef pair PII; const int N = 1000010; int idx,h[N],ne[N],w[N],e[N]; int dist[N]; bool st[N]; int n,m; void add(int a,int b,int c) { e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx ++; } int dijkstra() { memset(dist,0x3f,sizeof dist); dist[1] = 0; priority_queue heap;//堆里存储距离和节点编号 heap.push({0,1});//插入距离和节点编号 while(heap.size()) { auto t = heap.top();//取距离源点最近的点 heap.pop(); int distance = t.first,ver = t.second;//ver:节点编号，distance:源点距离ver 的距离 if(st[ver]) continue ;//如果距离已经确定，则跳过该点 st[ver] = true; for (int i = h[ver]; i != -1; i = ne[i] ) { int j = e[i]; if(dist[j] > dist[ver] + w[i]) { dist[j] = dist[ver] + w[i]; heap.push({dist[j], j}); } } } if(dist[n] == 0x3f3f3f3f) return -1; return dist[n]; } int main () { cin >> n >> m; memset(h, -1, sizeof h); while (m --) { int a,b,c; scanf("%d%d%d", &a, &b, &c); add(a, b, c); } printf("%d\n", dijkstra()); return 0; } 二、含负权边 Bellman-ford 【O(nm)】适用：限制边，有向，负权，稠密图 应用： 从A出发是否存在到达各个节点的路径(如果不是无穷则表示存在)； 从A出发到达各个节点最短路径(时间最少、路径最少…) 图中是否存在负环路（权重之和为负数） 题目链接 注意题目中限制了经过的边数 所以存在负权回路(转圈圈) 也不影响 松弛操作 其实就是更新当前最短距离，其中dist[]表示从起点到该点的距离。 w :权值 dist[b]=min(dist[b],dist[a]+w);
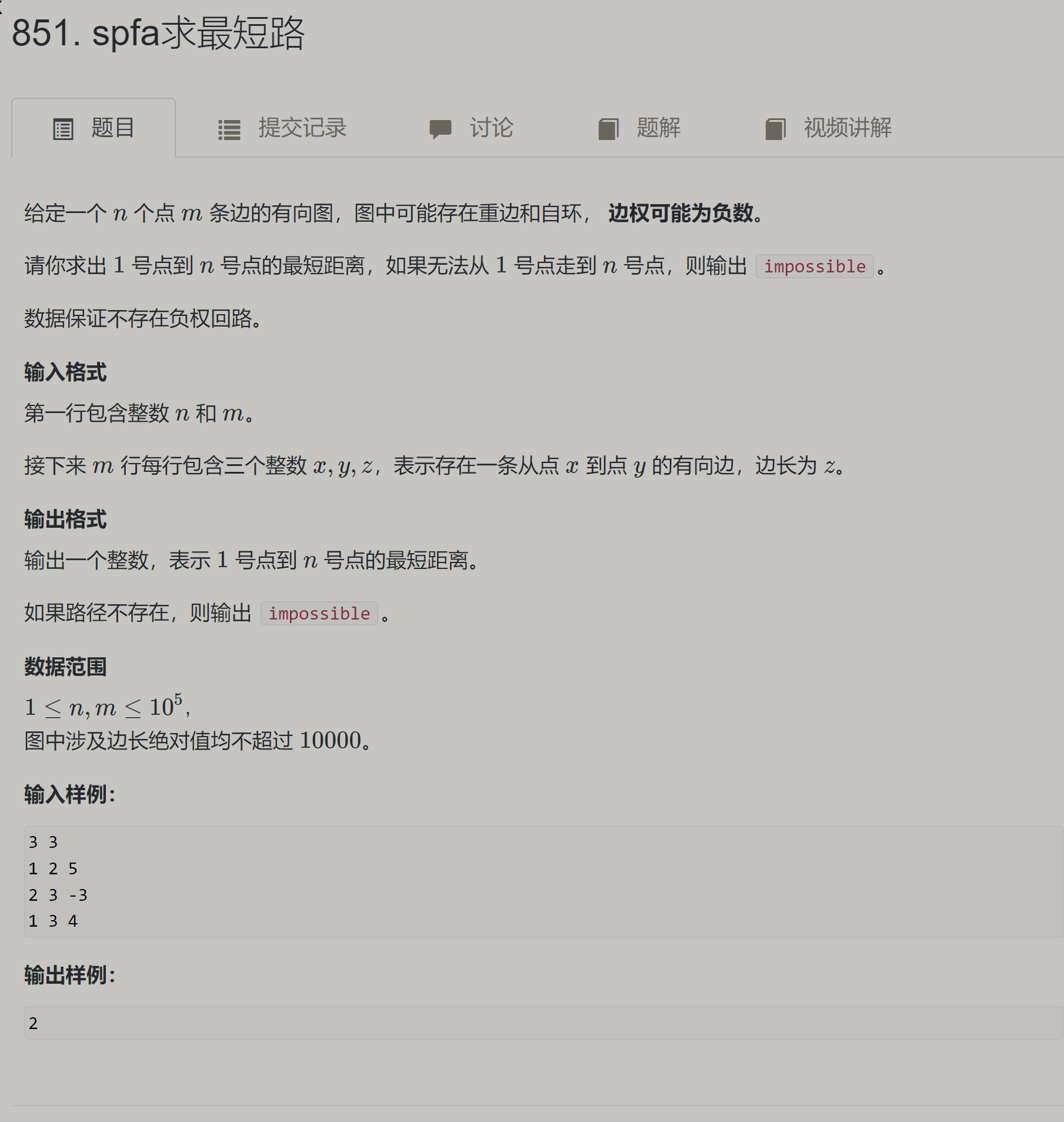
backup[j]表示每次进入第2重循环的dist数组的备份。 如果不加这个备份的话有可能会发生节点最短距离的串连 串联:就是多条边的值加到了一起。导致第k层循环之后找到一个边数大于k的路径。 如何理解迭代k次？ 其中迭代k次表示：不超过k条边的最短路径 正确的理解方式：迭代一次表示俩个结点只能通过一条边到达 如果迭代k次 就是 可以走k条边的最短路径 spfa求最短路【O(m) 最坏O(nm)】题目链接 思路和迪杰斯特拉堆优化差不多
这个也可以做dijkstraⅡ也能ac，而且还更快，手上的dijkstra瞬间不香了，但是如果是IO赛制最好还是用dijkstra，小心被出题人卡【y总的经验】 #include #include #include #include using namespace std; const int N = 100010; int idx,h[N],ne[N],w[N],e[N]; int dist[N]; bool st[N]; int n,m; void add(int a,int b,int c) { e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx ++; } void spfa() { memset(dist, 0x3f, sizeof dist); dist[1] = 0; queue q; q.push(1); st[1] = true;//存的是当前的点是否在队列当中 防止存负重复的点 while(q.size()) { int t = q.front(); q.pop(); st[t] = false; for (int i = h[t]; i != -1; i = ne[i] ) { int j = e[i]; if(dist[j] > dist[t] + w[i]) { dist[j] = dist[t] + w[i]; if(!st[j]) { q.push(j); st[j] = true; } } } } if(dist[n] == 0x3f3f3f3f) { puts("impossible"); } else { printf("%d\n", dist[n]); } } int main () { cin >> n >> m; memset(h, -1, sizeof h); while (m --) { int a,b,c; scanf("%d%d%d", &a, &b, &c); add(a, b, c); } spfa(); return 0; } spfa求负环基于上面的思路 ，多加了一个数组cnt[]，表示这个点存在的边数，根据抽屉原理可得该路线存在环，又因为求的是最短的边，所以只能是负环。 题目链接 Floyd 属于多源最短路径算法，能够求出任意2个顶点之间的最短路径，支持负权边，基于动态规划. 闫氏DP分析法: d[k,i,j] ：从i点出发，只经过k的点到达j的距离的所有集合。 属性：MIN 选：d[k - 1][i][j]//不经过k点 不选： f[k - 1][i][k] + [k - 1][k][j]//经过k点 状态转移方程(优化成一维):dist[i][j] = min(dist[i][j],dist[i][k] + dist[k][j]) C++代码 #include #include #include using namespace std; const int N = 210,INF = 1e9; int n, m, Q; int d[N][N]; void floyd() { for (int k = 1; k for (int j = 1; j scanf("%d%d%d", &n, &m, &Q); //初始化 for (int i = 1; i if(i == j) { d[i][j] = 0; } else { d[i][j] = INF; } } } while (m --) { int a, b, w; scanf("%d%d%d", &a, &b, &w); d[a][b] = min(d[a][b], w);//可能存在重边 } floyd(); while (Q --) { int a, b; scanf("%d%d", &a, &b); if(d[a][b] > INF / 2) { puts("impossible");//为什么是>=03xf3f3f3f/2?因为存在负权边 所以0x3f3f3f3f这个值可能会因为负值被更新 但值依然远大于0x3f3f3f3f/2 } else { printf("%d\n", d[a][b]); } } return 0; }文章参考——算法基础课 🌹感谢阅读🌹 |
【本文地址】
今日新闻 |
推荐新闻 |