数学 |
您所在的位置:网站首页 › ex泰勒展开式拉格朗日余项 › 数学 |
数学
|
欧拉公式
基础思想:无限的努力可以逼近成功。 通俗描述:仿造一条曲线,首先仿造它的初始点,然后是它的斜率,然后是它的二阶斜率。。不断递进。 数学定理: 链接:https://www.zhihu.com/question/25627482/answer/313088784 来源:知乎 先算个一阶的。 有一条解析式很复杂的曲线,我可以用多项式仿造一条曲线, 那么 f ( x ) ≈ g ( x ) = g ( x 0 ) + f 1 ( x 0 ) 1 ! ( x − x 0 ) + f 2 ( x 0 ) 2 ! ( x − x 0 ) 2 + . . . . . . + f n ( x 0 ) n ! ( x − x 0 ) n f(x) \approx g(x) =g(x_0)+\frac{f^1(x_0)}{1!}(x-x_0)+\frac{f^2(x_0)}{2!}(x-x_0)^2+......+\frac{f^n(x_0)}{n!}(x-x_0)^n f(x)≈g(x)=g(x0)+1!f1(x0)(x−x0)+2!f2(x0)(x−x0)2+......+n!fn(x0)(x−x0)n 泰勒指出:在实际操作过程中,可根据精度要求选择n值,只要n不是正无穷,那么,一定要保留上式中的约等号。若想去掉约等号,可写成下面形式: f ( x ) = g ( x ) = g ( x 0 ) + f 1 ( x 0 ) 1 ! ( x − x 0 ) + f 2 ( x 0 ) 2 ! ( x − x 0 ) 2 + . . . . . . f(x) = g(x) =g(x_0)+\frac{f^1(x_0)}{1!}(x-x_0)+\frac{f^2(x_0)}{2!}(x-x_0)^2+...... f(x)=g(x)=g(x0)+1!f1(x0)(x−x0)+2!f2(x0)(x−x0)2+...... 佩亚诺然后将误差的值通过泰勒展开中最小的一项进行限定。并求坐商。  可以看出,除了在 这个点,其他的都不重合,不满意。再来个二阶的。
可以看出,除了在 这个点,其他的都不重合,不满意。再来个二阶的。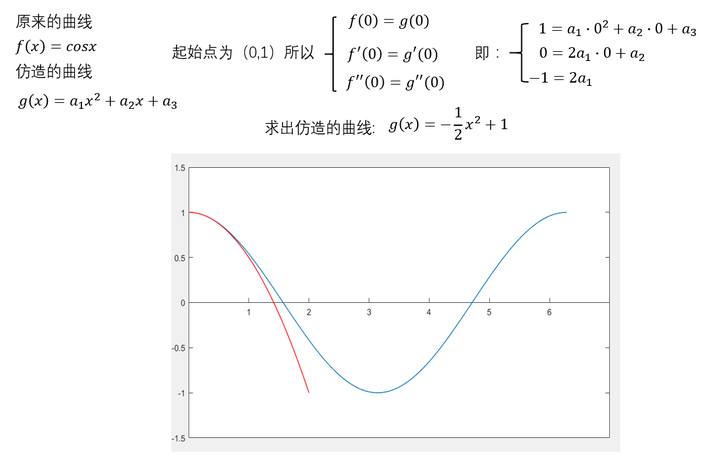 可以看出,在 这个点附近的一个小范围内,二者都比较相近。再来个四阶的。
可以看出,在 这个点附近的一个小范围内,二者都比较相近。再来个四阶的。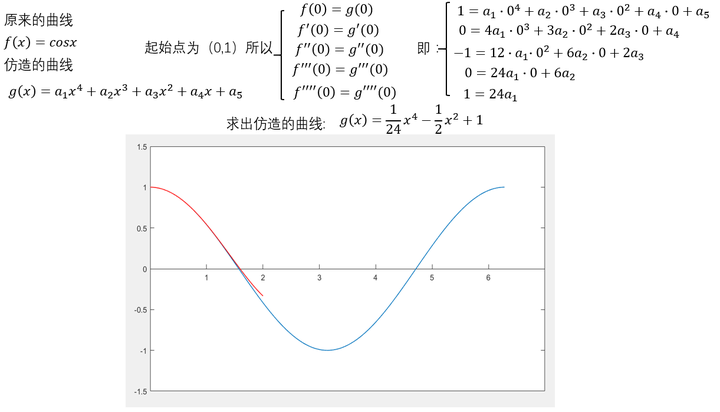 可以看出,仍然是在 这个点附近的一个范围内二者很相近。只是,此时二者重合的部分扩大了。到这里,不光是泰勒,我们普通人也能大概想象得到,如果继续继续提高阶数,相似范围继续扩大,无穷高阶后,整个曲线都无限相似。插个图,利用计算机可以快速实现。
可以看出,仍然是在 这个点附近的一个范围内二者很相近。只是,此时二者重合的部分扩大了。到这里,不光是泰勒,我们普通人也能大概想象得到,如果继续继续提高阶数,相似范围继续扩大,无穷高阶后,整个曲线都无限相似。插个图,利用计算机可以快速实现。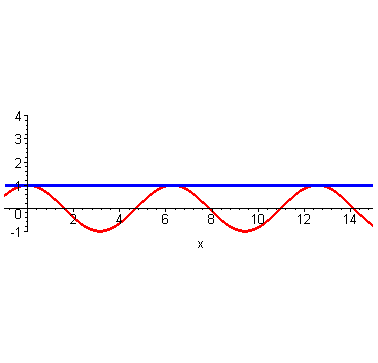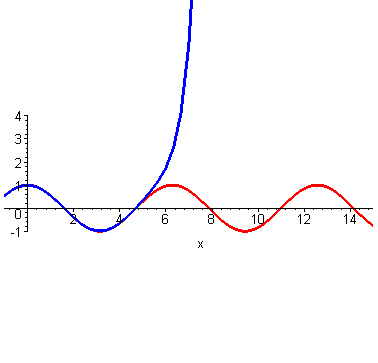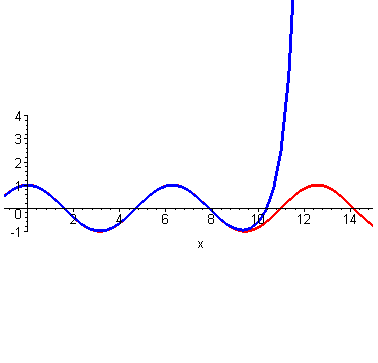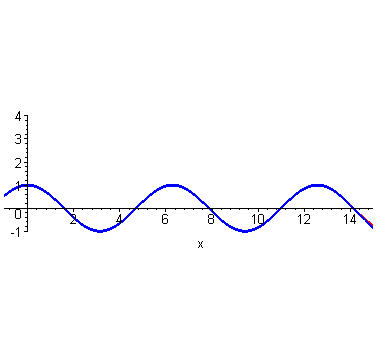
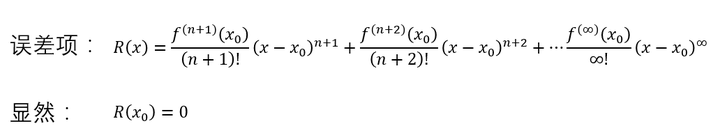 误差项 中每一项都是俩数的乘积,假如是你,你肯定是想两边同时除掉一个 ,对吧,为了简单,把 设为 :
误差项 中每一项都是俩数的乘积,假如是你,你肯定是想两边同时除掉一个 ,对吧,为了简单,把 设为 : 所以除过之后,就成了:
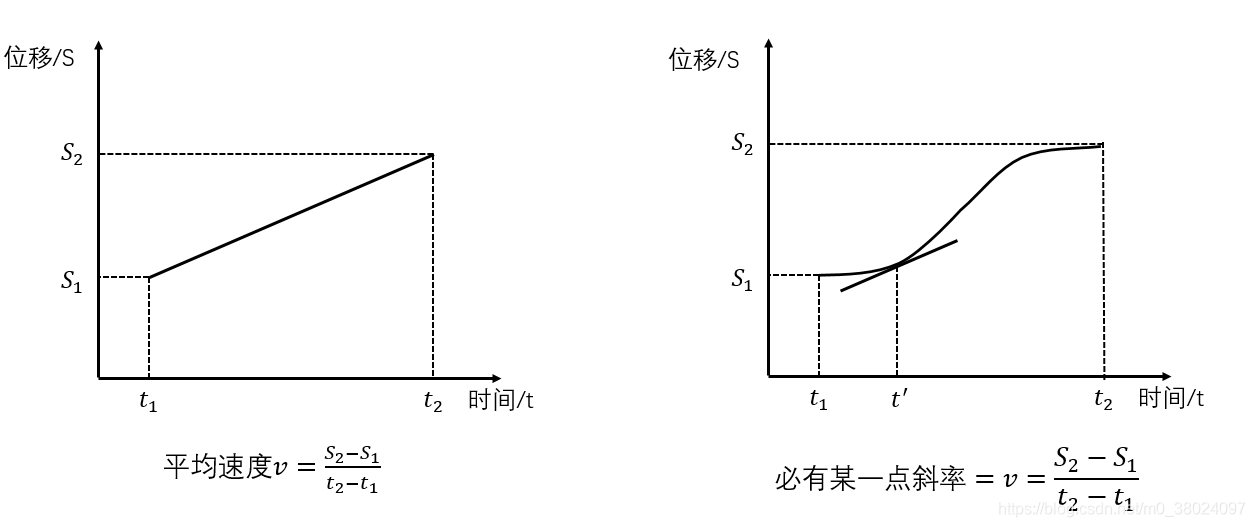
所以除过之后,就成了: 等等,这一串东西看着怎么眼熟?咦?这不是柯西老哥推广的我的中值定理么?剩下的不就是……:
等等,这一串东西看着怎么眼熟?咦?这不是柯西老哥推广的我的中值定理么?剩下的不就是……: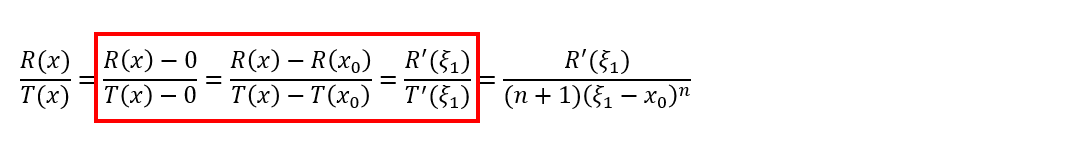 红框中,脑路之清奇、操作之风骚、画风之诡异、场面之震撼,让我们不禁感慨,拉格朗到底日了什么,脑海里才会想到柯西。拉格朗日写到这里卡住了,不知道你们有没有这种经验,反正我思考一道数学题的时候,会尝试着把思路进行到底,直到完全进了死胡同才会否定这种思路。有了前面的脑洞,拉格朗日继续复制这种思路,想看看能不能继续往下写:先看分子
红框中,脑路之清奇、操作之风骚、画风之诡异、场面之震撼,让我们不禁感慨,拉格朗到底日了什么,脑海里才会想到柯西。拉格朗日写到这里卡住了,不知道你们有没有这种经验,反正我思考一道数学题的时候,会尝试着把思路进行到底,直到完全进了死胡同才会否定这种思路。有了前面的脑洞,拉格朗日继续复制这种思路,想看看能不能继续往下写:先看分子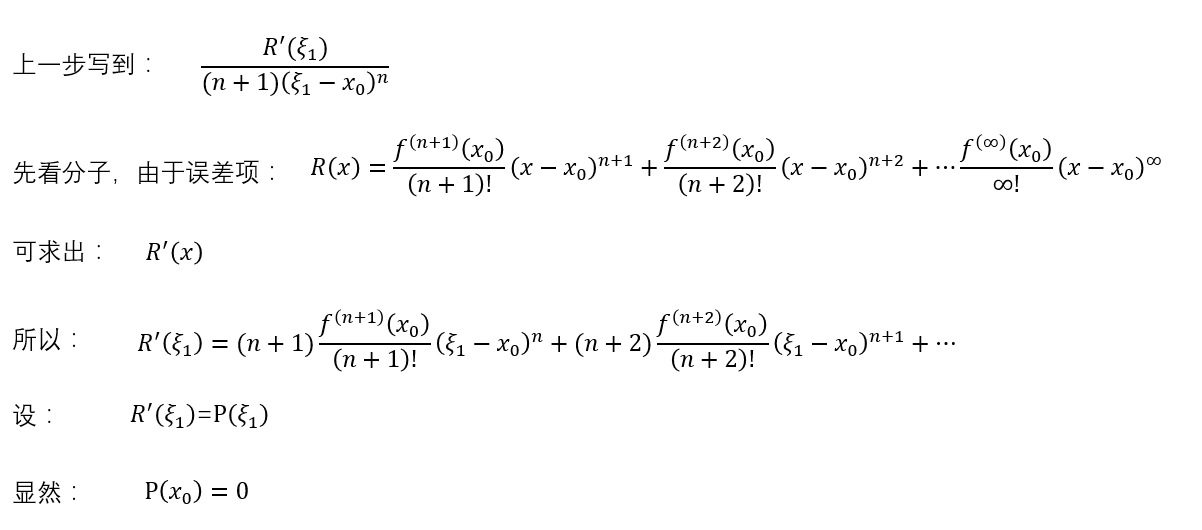 再看分母
再看分母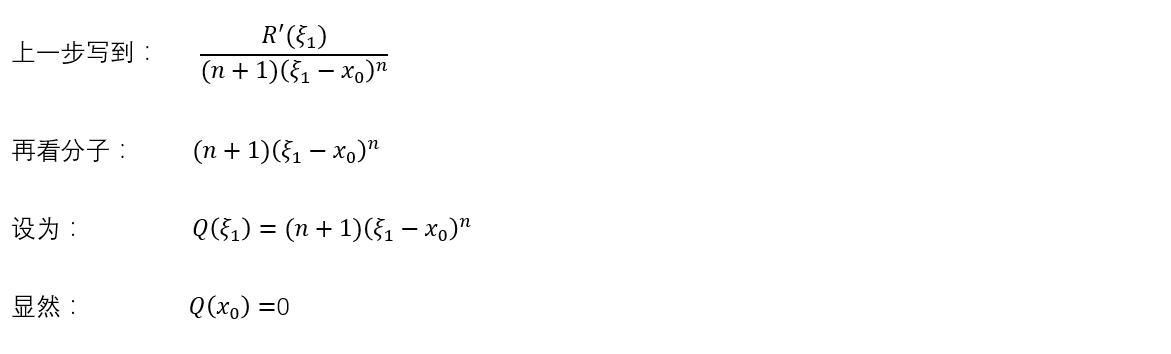 好巧合,又可以用一次柯西的中值定理了。
好巧合,又可以用一次柯西的中值定理了。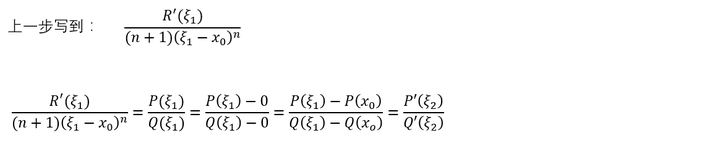 总之,按照这种方法,可以一直求解下去,最终的结果就是:至此,拉格朗日把后面无数多的误差项给整合成了一项,而且比配诺亚更加先进的地方在于,不一定非要让 趋近于 ,可以在二者之间的任何一个位置 处展开,及其好用。
总之,按照这种方法,可以一直求解下去,最终的结果就是:至此,拉格朗日把后面无数多的误差项给整合成了一项,而且比配诺亚更加先进的地方在于,不一定非要让 趋近于 ,可以在二者之间的任何一个位置 处展开,及其好用。