【最小生成树】一文学懂prim、kruskal算法 |
您所在的位置:网站首页 › dream的神级操作 › 【最小生成树】一文学懂prim、kruskal算法 |
【最小生成树】一文学懂prim、kruskal算法
|
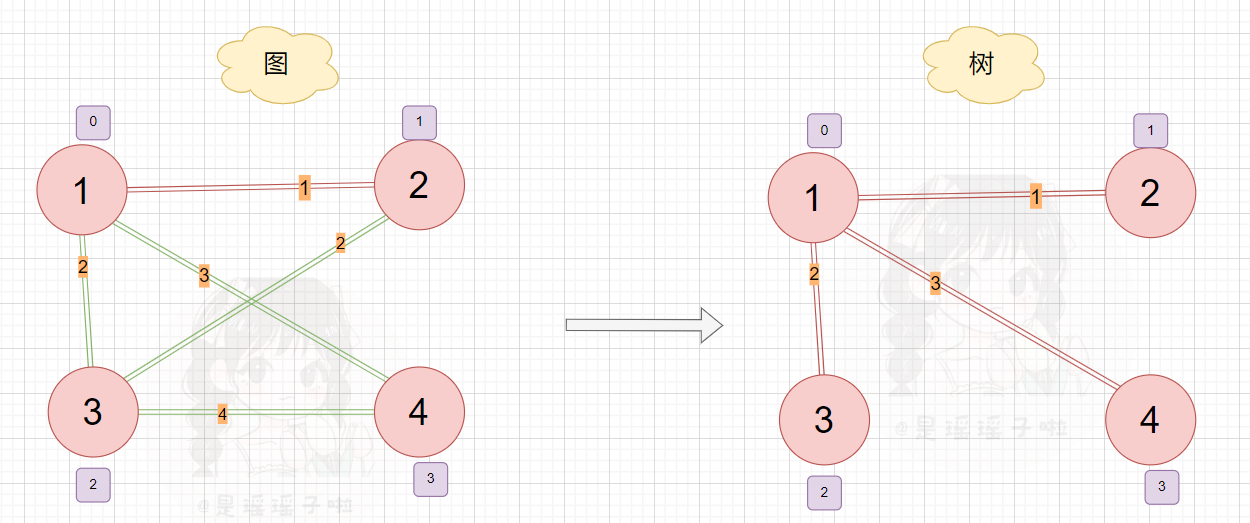
首先,我们要了解什么是最小生成树 🌠树and图? 其实树也是一种特殊的图;无向、无环、联通 图,就是树。 🌳最小生成树 求最小生成树,简单来说,就是让组成图的顶点,根据现有的边的关系,从图转换成一个特殊的图——树,光转换成树还不行,还要时这个特殊的图的所有边的权重加起来最小!这就是所谓的求最小生成树
每次将离连通部分的最近的点和点对应的边加入的连通部分,连通部分逐渐扩大,最后将整个图连通起来,并且边长之和最小。 📍首先一个dist数组,用于存储还为加入联通部分的点到联通部分的最短距离(绿色点表示未联通,红色表示已处于联通部分,紫色框中的是该点的dist值);最开始肯定所有点的dist都是无穷大(INF = 0x3f3f3f3f)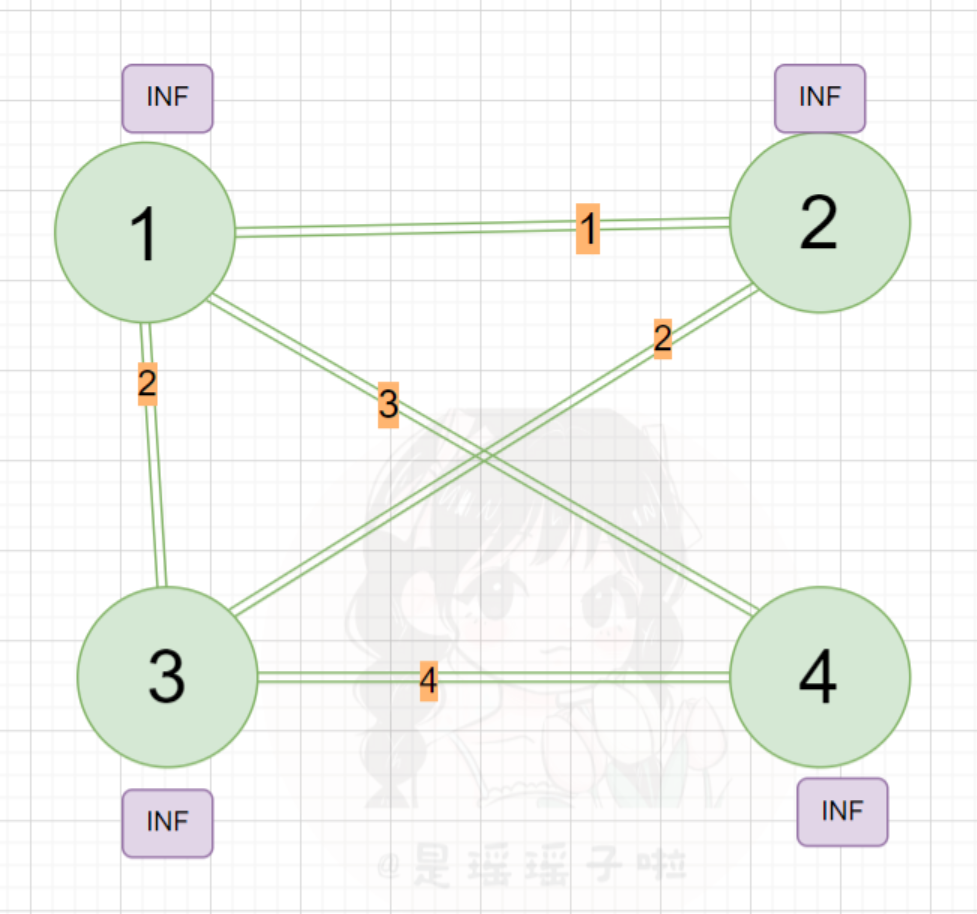 💡关于dist数组的定义,这里再用图形的方式来解释一下。红色表示已经暂时确定的连通图(也就是之后确定完全之后的最小生成树),绿色的表示某一个点,该点可能有很多条边连接到该连通图(也可能不能联通,不能联通就置为INF);取这些边中最小的一条,即为dist[E]就代表E点到联通图的最短距离 💡关于dist数组的定义,这里再用图形的方式来解释一下。红色表示已经暂时确定的连通图(也就是之后确定完全之后的最小生成树),绿色的表示某一个点,该点可能有很多条边连接到该连通图(也可能不能联通,不能联通就置为INF);取这些边中最小的一条,即为dist[E]就代表E点到联通图的最短距离 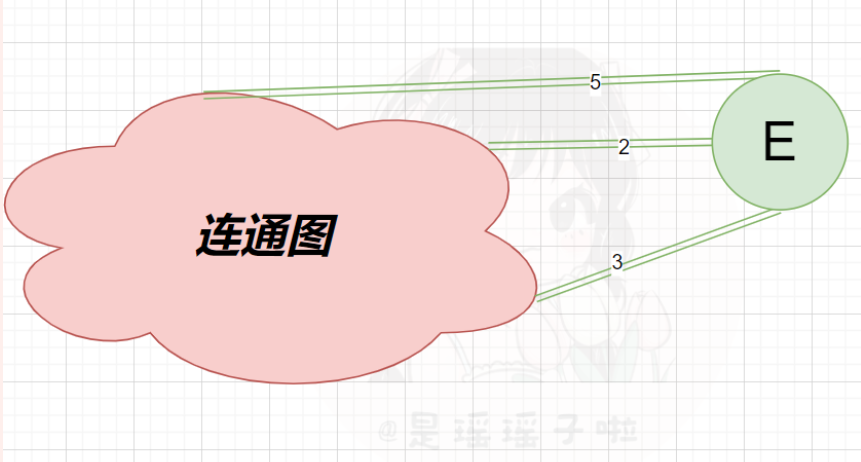 📍定义好dist数组并且初始化后,随便挑一个点都行,加入连通图集合,这里我们选入一号点加入集合,把dist[1]是0(后面代码并没有把第一个选中的点的dist置为0其实,直接不累加就行,第一个点的dist不用更新,也没有必要;注意在后续点进行时迭代时,必须先累加其dist,再更新,这点下面还会详细说) 📍定义好dist数组并且初始化后,随便挑一个点都行,加入连通图集合,这里我们选入一号点加入集合,把dist[1]是0(后面代码并没有把第一个选中的点的dist置为0其实,直接不累加就行,第一个点的dist不用更新,也没有必要;注意在后续点进行时迭代时,必须先累加其dist,再更新,这点下面还会详细说) 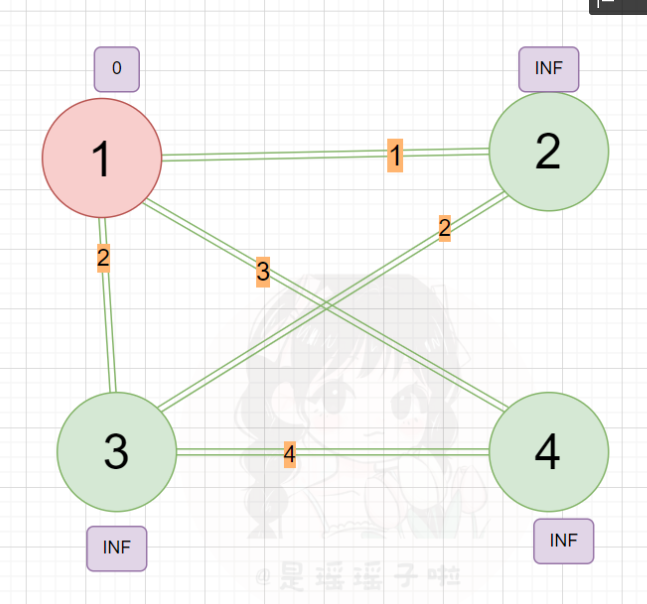 📍用找到的距离联通图距离最短的(未在联通图内,且dist最小)的该点,用该点遍历该点所连接的边的顶点,更新相邻点的dist!(和dijkstra有点像,先找到距离某个地方最近的一个点,用该点去更新相邻的其他点!) 📍用找到的距离联通图距离最短的(未在联通图内,且dist最小)的该点,用该点遍历该点所连接的边的顶点,更新相邻点的dist!(和dijkstra有点像,先找到距离某个地方最近的一个点,用该点去更新相邻的其他点!) 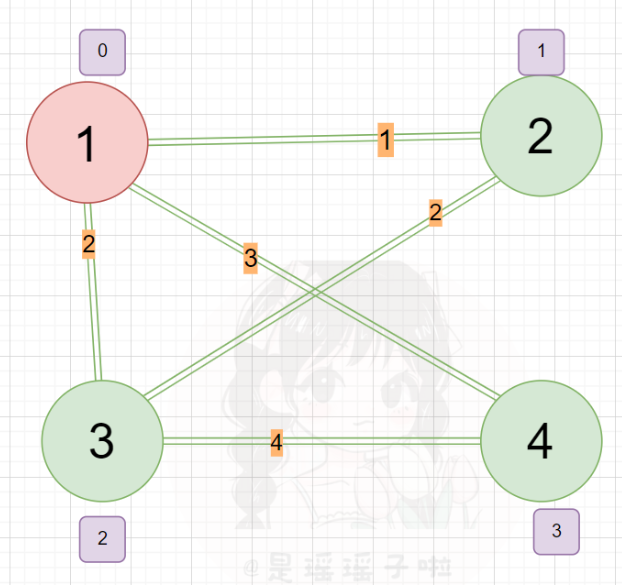 📍更新完后,下次迭代,先找到距离连通图距离最短的(这里就是2),用2更新相邻点到连通图的距离,再把2也加入联通图阵营📍不断进行上述找最小、借东风(以一点更新相邻点、加入联通图阵营(是不是和Dijkstra很像!不同的就在于,找最小和更新的部分)最后就形成了一个完整的、边数相加最小的联通图(即最小生成树) 📍更新完后,下次迭代,先找到距离连通图距离最短的(这里就是2),用2更新相邻点到连通图的距离,再把2也加入联通图阵营📍不断进行上述找最小、借东风(以一点更新相邻点、加入联通图阵营(是不是和Dijkstra很像!不同的就在于,找最小和更新的部分)最后就形成了一个完整的、边数相加最小的联通图(即最小生成树) 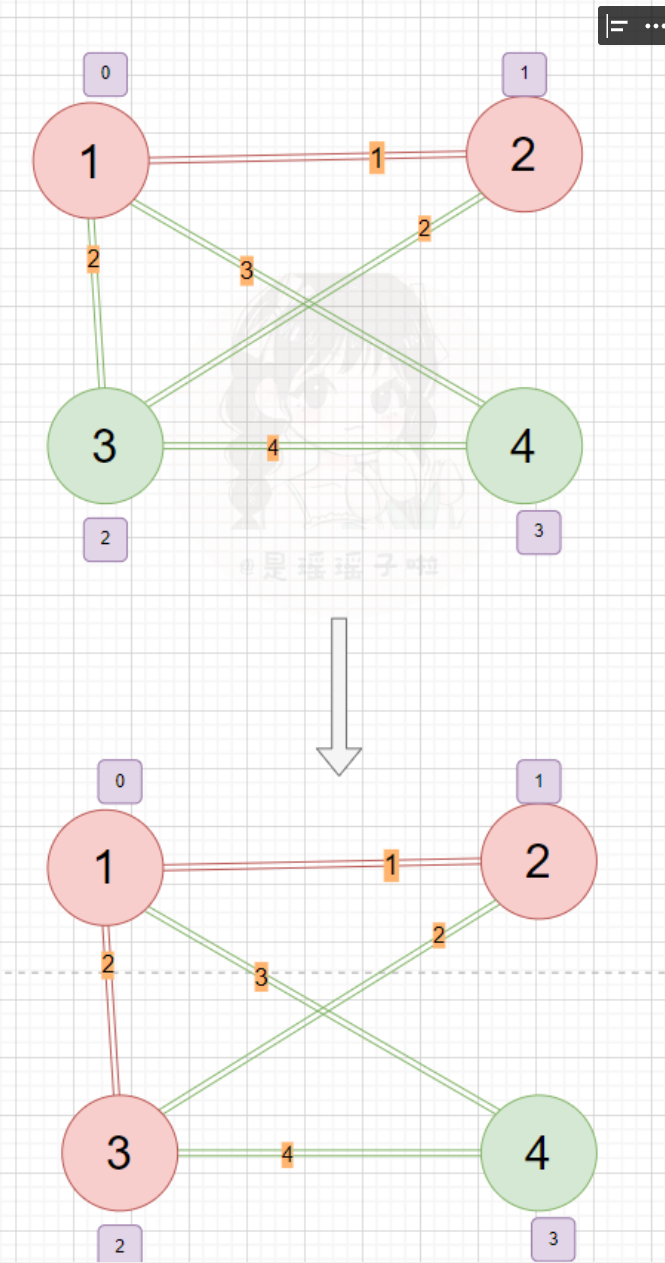 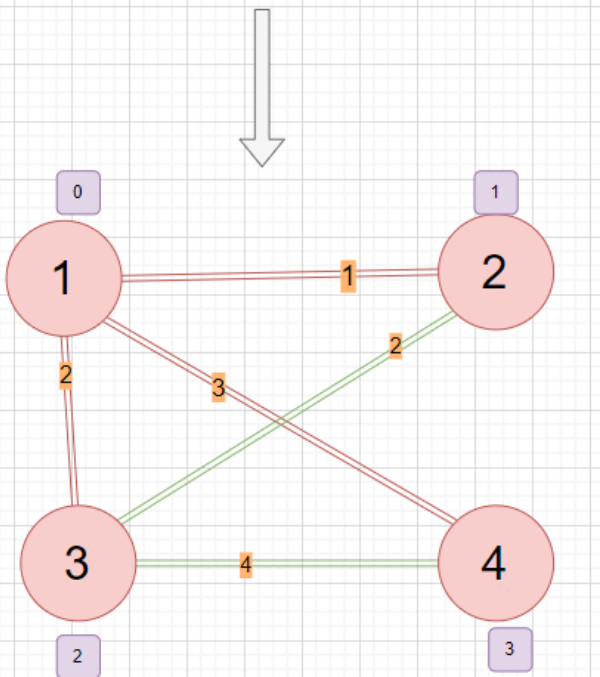 1.2:prim原理浅谈
1.2:prim原理浅谈
树是一种特殊的图,一个无向联通图且不包含回路(即不存在环),那么就是一个树 以下是菜鸟瑶瑶子的拙见 💡如何保证是个树? 首先一定不能有环,而且还得联通。这两点保证了,就是树。保证联通好说,在该算法中,我们把顶点一个一个依次往联通图上去连接,这个过程顺利进行就保证肯定是联通的。如何保证没有环呢?可以这样理解,一个顶点有两只手,一个点加入联通图,那么一只手就和联通图连上了,如果再把该点再次加入联通图(另一只手也连上),那势必会存在环。而该算法保证每次往联通图中加的点都是不在联通图中的。这就保证了在联通图中的点,一只手连着联通图,另一只手空着或者连着联通图外的点。这样一来,就不会存在环了 💡如何保证边的和最小? 其实是贪心策略。局部最优,我们每次往联通图中加入的点,都是离联通图最近的点。局部最优解构成全局最优解(因为目前还没学到贪心,要真说原理什么的,我目前还证明不了,只能凭着感觉去意会,感兴趣的同学可以上C站或者百度搜搜看) 1.3:核心模板代码from acwing(侵删) 时间复杂度是 O(n2+m)O(n2+m), n 表示点数,m 表示边数 时间复杂度是 O(n2+m)O(n2+m), nn 表示点数,mm 表示边数 int n; // n表示点数 int g[N][N]; // 邻接矩阵,存储所有边 int dist[N]; // 存储其他点到当前最小生成树的距离 bool st[N]; // 存储每个点是否已经在生成树中 // 如果图不连通,则返回INF(值是0x3f3f3f3f), 否则返回最小生成树的树边权重之和 int prim() { memset(dist, 0x3f, sizeof dist); int res = 0; for (int i = 0; i memset(dist,0x3f, sizeof dist); int res = 0; for(int i = 0;i scanf("%d%d",&n,&m); memset(g,0x3f, sizeof g); while(m--){ int a,b,c; scanf("%d%d%d",&a,&b,&c); g[a][b] = g[b][a] = min(g[a][b],c);//存边,无向图,记得存两条边,且要判重 } int t = prim(); if(t == INF) puts("impossible"); else printf("%d\n",t); return 0; }💡注意点 与dijkstra不同,prim需要迭代n次(因为dijkstra已经确定的起点,少的那一次就少在,dijkstra在循环前就把源点加入集合了!)最小生成树是针对无向图的,所以在读入边的时候,需要赋值两次(且注意判重!)要先把这次迭代选中的点的dist累加,再已该点更新与之相连的点,避免t有自环(在更新的适合dist[t] = 0,后面再累加进答案就不对了),影响答案的正确性。后更新不会影响后面的结果么?不会的,因为dist[i]为i到集合S的距离,当t放入集合后,其dist[t]就已经没有意义了,再更新也不会影响答案的正确性 📌二、kruskal算法 2.1基本思路核心思想::所有边能小则小,算法的实现方面要用到***并查集***判断两点是否在同一集合 首先,将所有边,按照权重大小,从小到大排序 构造一个只含 n 个顶点、而边集为空的子图,把子图中各个顶点看成各棵树上的根结点 从边集 E 中选取一条权值最小的边,若该条边的两个顶点分属不同的树(保证了最后是联通且没有环的图,即树),则将其加入子图;即把两棵树合成一棵树; 反之,若该条边的两个顶点已落在同一棵树上,则不可取(取了的话会形成环!),而应该取下一条权值最小的边再试之 依次类推,直到森林中只有一棵树,也即子图中含有 n-1 条边为止。 2.2:具体步骤/实现将图中所有边对象(边长、两端点)依次加入集合(优先队列)q1中(或者用数组存边,之后再按权重排序一下,本质都是一样的,让所有的边按升序存储)。初始所有点相互独立(都是不同树的根节点) 取出存储边的集合中的最小边,判断边的两点是否联通。(是否同属于一棵树/集合/连通块 如果联通说明两个点已经有其它边将两点联通了,跳过(不然就形成自环啦),如果不连通,则使用并查集合并,将两个顶点合并 重复2,3操作直到存储边的集合为空。此时被选择的边构成最小生成树。 2.3算法模板from acwing(侵删) 时间复杂度是 O(mlogm)O(mlogm), n 表示点数,m 表示边数 int n, m; // n是点数,m是边数 int p[N]; // 并查集的父节点数组 struct Edge // 存储边 { int a, b, w; bool operator if (p[x] != x) p[x] = find(p[x]); return p[x]; } int kruskal() { sort(edges, edges + m); for (int i = 1; i p[a] = b; res += w; cnt ++ ; } } if (cnt return this->w for (int i = 1; i //a和b两个点暂时不在一个连通块,符合! res += edge[i].w; p[pa] = pb;//合并a,b两个集合 cnt ++;//最终连通块的边数+1 } } } int main(){ cin >> n >> m; for(int i = 1; i a,b,c}; } //对每条边,按照权重进行从小到大排序(升序 sort(edge+1, edge + m +1);//[ edge[1], edge[m+1] ) 左闭右开 kruskal(); if(cnt |
【本文地址】
今日新闻 |
推荐新闻 |