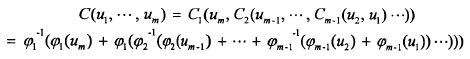“Copula”一词源于拉丁语，意为“联结、联系”。最初由Sklar在1959年提出，被广泛应用于统计、金融、风险管理等领域。Copula是处理统计中随机变量相关性问题的一种方法。

  在一般情形下， n n n元 Copula函数 C : [ 0 , 1 ] n → [ 0 , 1 ] C:[0,1]^n\rightarrow[0,1] C:[0,1]n→[0,1]是多元联合分布 C ( u 1 , u 2 , . . . , u n ) = P ( U 1 ≤ u 1 , U 2 ≤ u 2 , . . . , U n ≤ u n ) C(u_1,u_2,...,u_n)=P(U_1\leq u_1,U_2\leq u_2,...,U_n\leq u_n) C(u1​,u2​,...,un​)=P(U1​≤u1​,U2​≤u2​,...,Un​≤un​)

其中 U 1 , U 2 , . . . , U n U_1,U_2,...,U_n U1​,U2​,...,Un​是标准均匀变量。

  Copula 有连接和交换的意思，因此Copula函数又被称作连接函数，Nelsen [ 4 ] ^{[4]} [4]在1998年给出了Copula函数的定义，指出具有下面性质的函数C是N维Copula函数。

Sklar定理

  设 H H H是 n n n维随机变量 ( X 1 , . . . , X n ) (X_1,...,X_n) (X1​,...,Xn​)的联合分布函数，与其对应的边际分布分别是 F 1 , . . . , F n F_1,...,F_n F1​,...,Fn​，则存在一个 n n n元Copula函数 C C C使得对于全部 ( x 1 , x 2 , . . . , x n ) ∈ [ − ∞ , + ∞ ] n (x_1,x_2,...,x_n)\in[-\infty,+\infty]^n (x1​,x2​,...,xn​)∈[−∞,+∞]n，有 H ( x 1 , x 2 , . . . , x n ) = C ( F 1 ( x 1 ) , F 2 ( x 2 ) , . . . , F n ( x n ) ) ( 1 ) H(x_1,x_2,...,x_n)=C(F_1(x_1),F_2(x_2),...,F_n(x_n))\quad\quad(1) H(x1​,x2​,...,xn​)=C(F1​(x1​),F2​(x2​),...,Fn​(xn​))(1)

若 F 1 , . . . , F n F_1,...,F_n F1​,...,Fn​是连续的，则 C C C唯一；否则 C C C仅在 R a n ( F 1 ) × . . . × R a n ( F n ) Ran(F_1)\times...\times Ran(F_n) Ran(F1​)×...×Ran(Fn​)上唯一。

反之

  若 C C C是一个Copula函数， F 1 , . . . , F n F_1,...,F_n F1​,...,Fn​是单变量分布函数，则(1)式定义的 H ( x 1 , x 2 , . . . , x n ) H(x_1,x_2,...,x_n) H(x1​,x2​,...,xn​)是边缘分布为 F 1 , . . . , F n F_1,...,F_n F1​,...,Fn​的随机向量的联合分布函数。

【说明】 定理给出了一种利用边际分布对多元联合分布建模的方法：（1）构建各变量的边际分布；（2）找到一个恰当的Copula函数，确定它的参数，作为刻画各个变量之间相关关系的工具。

推论

  设随机变量 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1​,X2​,...,Xn​的分布函数 F 1 ( x 1 ) , F 2 ( x 2 ) , . . . , F n ( x n ) F_1(x_1),F_2(x_2),...,F_n(x_n) F1​(x1​),F2​(x2​),...,Fn​(xn​)均是连续的， U 1 = F 1 ( X 1 ) , . . . , U n = F n ( X n ) U_1=F_1(X_1),...,U_n=F_n(X_n) U1​=F1​(X1​),...,Un​=Fn​(Xn​)均服从 [ 0 , 1 ] [0,1] [0,1]上的均匀分布，则随机变量 U 1 , . . . , U n U_1,...,U_n U1​,...,Un​的联合分布为 C ( u 1 , u 2 , . . . , u n ) = H ( F 1 − 1 ( u 1 ) , F 2 − 2 ( u 2 ) , . . . , F n − 1 ( u n ) ) = P ( U 1 ≤ u 1 , U 2 ≤ u 2 , . . . , U n ≤ u n ) ( 2 ) \begin{aligned} C(u_1,u_2,...,u_n)&=H(F_1^{-1}(u_1),F_2^{-2}(u_2),...,F_n^{-1}(u_n))\\ &=P(U_1\leq u_1,U_2\leq u_2,...,U_n\leq u_n) \end{aligned}\quad\quad(2) C(u1​,u2​,...,un​)​=H(F1−1​(u1​),F2−2​(u2​),...,Fn−1​(un​))=P(U1​≤u1​,U2​≤u2​,...,Un​≤un​)​(2)

其中 F i − 1 ( u i ) F_i^{-1}(u_i) Fi−1​(ui​)称为 F i F_i Fi​的伪逆函数，定义为 F i ( u ) = i n f { x : F ( x ) ≥ u } F_i(u)=inf\{x:F(x)\geq u\} Fi​(u)=inf{x:F(x)≥u}

【说明】 设 F 1 , . . . , F n F_1,...,F_n F1​,...,Fn​是连续的，联合分布函数也已经知道，用(2)式完全可以构造出相应的Copula函数，并且构造出的Copula函数完全刻画了变量之间的相依结构。

  设一个 n n n维向量 ( X 1 , . . . , X n ) (X_1,...,X_n) (X1​,...,Xn​)的边缘密度函数是 f i ( x i ) f_i(x_i) fi​(xi​)，联合密度是 f ( x 1 , x 2 , . . . , x n ) = ∂ n F ( x 1 , x 2 , . . . , x n ) ∂ x 1 ∂ x 2 . . . ∂ x n f(x_1,x_2,...,x_n)=\frac{\partial^nF(x_1,x_2,...,x_n)}{\partial x_1\partial x_2...\partial x_n} f(x1​,x2​,...,xn​)=∂x1​∂x2​...∂xn​∂nF(x1​,x2​,...,xn​)​

Copula函数 C C C的密度为 c ( u 1 , u 2 , . . . , u n ) = ∂ n C ( u 1 , u 2 , . . . , u n ) ∂ u 1 ∂ u 2 . . . ∂ u n c(u_1,u_2,...,u_n)=\frac{\partial^nC(u_1,u_2,...,u_n)}{\partial u_1\partial u_2...\partial u_n} c(u1​,u2​,...,un​)=∂u1​∂u2​...∂un​∂nC(u1​,u2​,...,un​)​

则有 f ( x 1 , x 2 , . . . , x n ) = c ( F 1 ( x 1 ) , F 2 ( x 2 ) , . . . , F n ( x n ) ) × ∏ i = 1 n f i ( x i ) f(x_1,x_2,...,x_n)=c(F_1(x_1),F_2(x_2),...,F_n(x_n))\times\prod_{i=1}^{n}f_i(x_i) f(x1​,x2​,...,xn​)=c(F1​(x1​),F2​(x2​),...,Fn​(xn​))×i=1∏n​fi​(xi​)

  双参数Copula函数有很多种，双参数BB1和BB7 Copula能够较好的刻画尾部相依结构，它们的数学形式如下：

BB1: C ( u , v , θ , δ ) = { 1 + [ ( u − θ − 1 ) δ + ( v − θ − 1 ) δ ] 1 / δ } − 1 / θ C(u,v,\theta,\delta)=\{1+[(u^{-\theta}-1)^\delta+(v^{-\theta}-1)^\delta]^{1/\delta}\}^{-1/\theta} C(u,v,θ,δ)={1+[(u−θ−1)δ+(v−θ−1)δ]1/δ}−1/θ， θ ∈ ( 0 , ∞ ) , δ ∈ [ 1 , ∞ ] \theta\in(0,\infty),\delta\in[1,\infty] θ∈(0,∞),δ∈[1,∞]

BB7: C ( u , v , θ , δ ) = 1 − ( 1 − ( ( 1 − u − θ ) − δ + ( 1 − v − θ ) − δ − 1 ) − 1 / δ ) 1 / θ C(u,v,\theta,\delta)=1-(1-((1-u^{-\theta})^{-\delta}+(1-v^{-\theta})^{-\delta}-1)^{-1/\delta})^{1/\theta} C(u,v,θ,δ)=1−(1−((1−u−θ)−δ+(1−v−θ)−δ−1)−1/δ)1/θ， θ ∈ [ 1 , ∞ ] , δ ∈ ( 0 , ∞ ) \theta\in[1,\infty],\delta\in(0,\infty) θ∈[1,∞],δ∈(0,∞)

其中 θ \theta θ、 δ \delta δ为双参数Copula的两个参数。

  Copula 函数能够把随机变量之间的相关关系与变量的边际分布分开进行研究，这种思想方法在多元统计分析中非常重要。直观地来看，可以将任意维的联合分布 H ( x 1 , . . . , x n ) = P ( X 1 ≤ x 1 , . . . , X n ≤ x n ) H(x_1,...,x_n)=P(X_1\leq x_1,...,X_n\leq x_n) H(x1​,...,xn​)=P(X1​≤x1​,...,Xn​≤xn​)分成两步来处理。第一是，对所有的单变量随机变量 X i X_i Xi​，通过累积分布函数 F i F_i Fi​，我们可以得到随机变量 U i = F i ( X i ) U_i=F_i(X_i) Ui​=Fi​(Xi​)，这是一个均匀随机变量；第二是，随机变量间的相依结构能够通过直接连接这些均匀变量的 n n n元Copula函数 C ( u 1 , . . . , u n ) C(u_1,...,u_n) C(u1​,...,un​)来描述。 [ 1 ] ^{[1]} [1]

  Copula函数是定义域为 [ 0 , 1 ] [0,1] [0,1]均匀分布的多维联合分布函数，其核心概念是以Copula函数将多个随机变量的边缘分布耦合起来。Copula函数本质上是边缘分布为 F X 1 ( x 1 ) , F X 2 ( x 2 ) , . . . , F X N ( x N ) F_{X_1}(x_1),F_{X_2}(x_2),...,F_{X_N}(x_N) FX1​​(x1​),FX2​​(x2​),...,FXN​​(xN​)的随机变量 X 1 , X 2 , . . . , X N X_1,X_2,...,X_N X1​,X2​,...,XN​的多元联合分布函数。因此求取联合分布函数即为确定函数C，Copula函数理论为求解多个随机变量联合概率分布提供了新的思路和工具。 [ 2 ] ^{[2]} [2]

  考察两个随机变量 X X X和 Y Y Y，其连续累积分布函数分别为 F X F_X FX​和 F Y F_Y FY​。通过分别在两个随机变量上应用概率积分变换，得到 U = F X ( X ) U=F_X(X) U=FX​(X)和 V = F Y ( Y ) V=F_Y(Y) V=FY​(Y)。 U U U和 V V V都是服从 [ 0 , 1 ] [0,1] [0,1]上均匀分布的变量，它们的相关性取决于 X X X和 Y Y Y是否相关：如果 X X X和 Y Y Y是不相关的，那么 U U U和 V V V也是不相关的，因为这个转换是可逆的，定义 X X X和 Y Y Y之间的相关性等价于 U U U和 V V V之间的相关性。由于 U U U和 V V V是均匀分布的随机变量，所以问题被简化为定义一个在两个均匀分布之上的联合分布，这就是 Copula。Copula 函数的基本思想就是，通过把边缘变量转化为均匀分布变量而不再需要考察很多不同的边缘分布以简化问题，然后再把相关性定义为一个在均匀分布之上的联合分布。

  定义二维Copula函数 C C C为 I 2 → I , I = [ 0 , 1 ] I^2\rightarrow I, I=[0,1] I2→I,I=[0,1]上的一个映射，满足以下性质：

  Copula函数总体上可以划分为Archimedean型、椭圆型和二次型。

  Archimedean Copula函数主要分为对称型和非对称型两大类。

对称型Archimedean Copula函数

  对称型Archimedean Copula函数简称SAC，其m维结构为： C ( u 1 , u 2 , . . . , u n ) = φ − 1 ( φ ( u 1 ) + φ ( u 2 ) + . . . 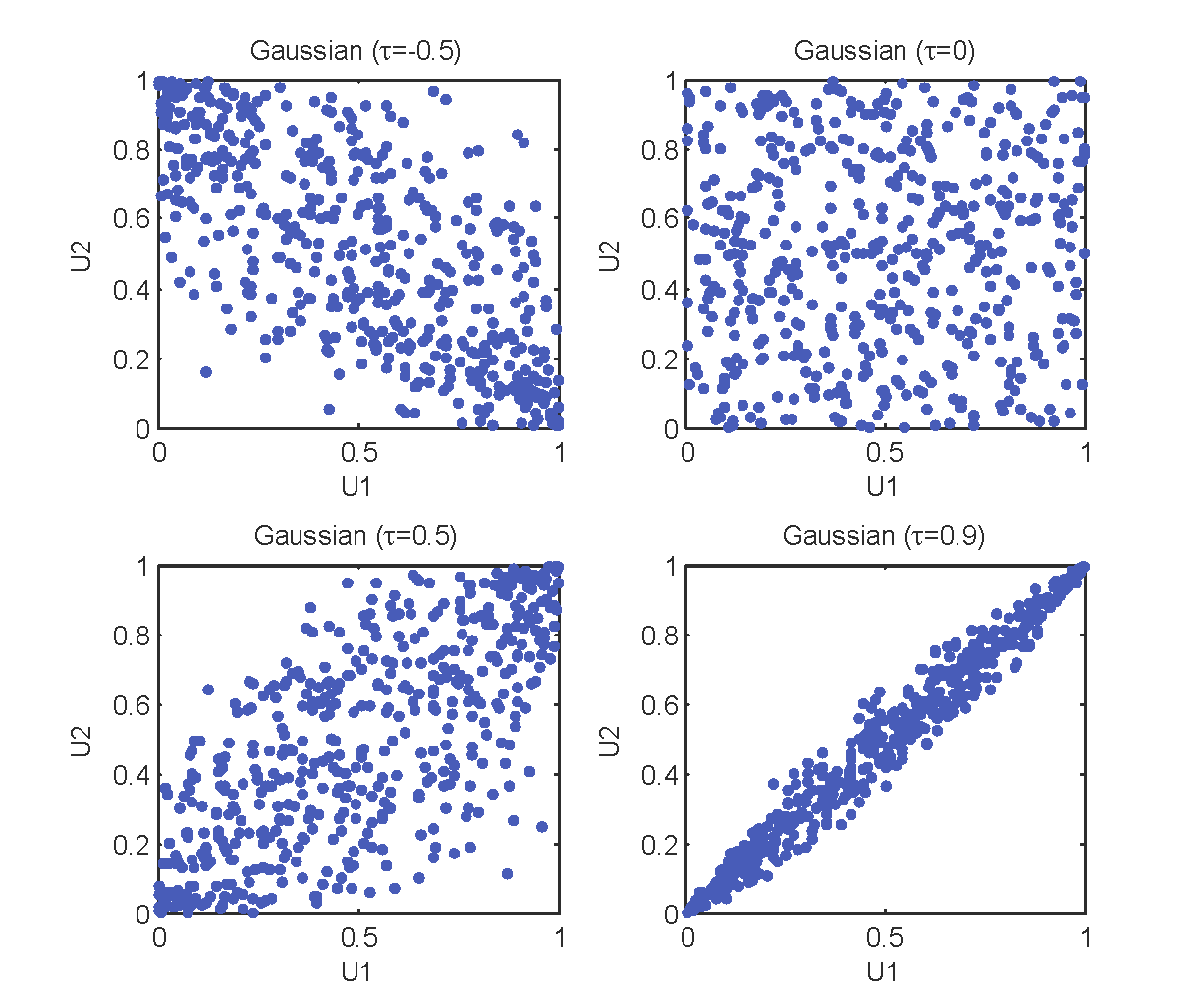+ φ ( u m ) ) C(u_1,u_2,...,u_n)=\varphi^{-1}(\varphi(u_1)+\varphi(u_2)+...+\varphi(u_m)) C(u1​,u2​,...,un​)=φ−1(φ(u1​)+φ(u2​)+...+φ(um​)) 式中， φ \varphi φ满足： φ ( 0 ) = ∞ , φ ( 1 ) = 0 \varphi(0)=\infty, \varphi(1)=0 φ(0)=∞,φ(1)=0，对 ∀ 0 ≤ t ≤ 1 \forall 0\leq t\leq1 ∀0≤t≤1，有 φ ′ ( t ) < 0 , φ ′ ′ ( t ) > 0 \varphi'(t)0 φ′(t)0。可见Copula函数由生成函数决定。以二维为例，常见的对称型Archimedean Copula函数如下表所列。 非对称型Archimedean Copula函数

  非对称型Archimedean Copula函数简称AAC，适用于构建三维以上Copula函数，其m维非对称Copula结构表示如下：

  Fang等首先提出了椭圆Copula函数的概念，并对其进行了详细的阐述。Gaussian Copula函数和Student t Copula函数是最常用的椭圆Copula函数。

高斯Copula函数

  二元高斯Copula函数： C ( u , v ) = Φ ρ ( Φ − 1 ( u ) , Φ − 1 ( v ) ) C(u,v)=\Phi_\rho(\Phi^{-1}(u),\Phi^{-1}(v)) C(u,v)=Φρ​(Φ−1(u),Φ−1(v)) 其中 Φ ρ \Phi_\rho Φρ​是相关系数为 ρ \rho ρ的二维高斯分布的分布函数， Φ \Phi Φ是标准正态分布函数。

  下图是不同相关参数下高斯Copula的散点图。

   n n n元高斯Copula函数： C ( u 1 , u 2 , . . . , u n ; Σ ) = Φ Σ ( Φ − 1 ( u 1 ) , . . . , Φ − 1 ( u n ) ) = ∫ − ∞ Φ − 1 ( u 1 ) . . . ∫ − ∞ Φ − 1 ( u n ) 1 ( 2 π ) d 2 ∣ Σ ∣ 1 2 e x p ( − 1 2 W T Σ − 1 W ) d W \begin{aligned} C(u_1,u_2,...,u_n;\Sigma)&=\Phi_\Sigma(\Phi^{-1}(u_1),...,\Phi^{-1}(u_n))\\ &=\int_{-\infty}^{\Phi^{-1}(u_1)}...\int_{-\infty}^{\Phi^{-1}(u_n)}\frac{1}{(2\pi)^{\frac{d}{2}}|\Sigma|^{\frac{1}{2}}}exp\left(-\frac{1}{2}W^T\Sigma^{-1}W\right)dW \end{aligned} C(u1​,u2​,...,un​;Σ)​=ΦΣ​(Φ−1(u1​),...,Φ−1(un​))=∫−∞Φ−1(u1​)​...∫−∞Φ−1(un​)​(2π)2d​∣Σ∣21​1​exp(−21​WTΣ−1W)dW​ 式中， Φ ( ⋅ ) \Phi(\cdot) Φ(⋅)为标准正态分布函数； Φ Σ ( Φ − 1 ( u 1 ) , . . . , Φ − 1 ( u n ) ) \Phi_\Sigma(\Phi^{-1}(u_1),...,\Phi^{-1}(u_n)) ΦΣ​(Φ−1(u1​),...,Φ−1(un​))为均值为0、协方差为 Σ \Sigma Σ的正态分布函数； Σ = [ 1 . . . ρ 1 n . . . . . . . . . ρ n 1 . . . 1 ] \Sigma=\left[\begin{matrix} 1&...&\rho_{1n}\\ ...&...&...\\ \rho_{n1}&...&1 \end{matrix}\right] Σ=⎣⎡​1...ρn1​​.........​ρ1n​...1​⎦⎤​， ρ i j = { 1 ; i = j ρ i j ; i ≠ j , − 1 ≤ ρ i j ≤ 1 \rho_{ij}=\left\{\begin{matrix} 1; i=j\\\rho_{ij}; i\neq j \end{matrix}\right., -1\leq \rho_{ij}\leq1 ρij​={1;i=jρij​;i​=j​,−1≤ρij​≤1； W = [ w 1 , w 2 , . . . , w n ] W=[w_1,w_2,...,w_n] W=[w1​,w2​,...,wn​]为积分变量矢量。

  其Copula密度为 c ( u 1 , u 2 , . . . , u n ; Σ ) = ∂ C ( u 1 , u 2 , . . . , u n ; Σ ) ∂ u 1 . . . ∂ u n = 1 ∣ Σ ∣ 1 / 2 e x p { − 1 2 [ Φ − 1 ( u 1 ) , . . . , Φ − 1 ( u n ) ] Σ − 1 ( Φ − 1 ( u 1 ) . . . Φ − 1 ( u n ) ) + 1 2 ∑ i = 1 n ( Φ − 1 ( u i ) ) 2 } \begin{aligned} c(u_1,u_2,...,u_n;\Sigma)&=\frac{\partial C(u_1,u_2,...,u_n;\Sigma)}{\partial u_1...\partial u_n}\\ &=\frac{1}{|\Sigma|^{1/2}}exp\{-\frac{1}{2}[\Phi^{-1}(u_1),...,\Phi^{-1}(u_n)]\Sigma^{-1}\left(\begin{matrix} \Phi^{-1}(u_1)\\ ...\\ \Phi^{-1}(u_n) \end{matrix}\right)+\frac{1}{2}\sum_{i=1}^{n}(\Phi^{-1}(u_i))^2\} \end{aligned} c(u1​,u2​,...,un​;Σ)​=∂u1​...∂un​∂C(u1​,u2​,...,un​;Σ)​=∣Σ∣1/21​exp{−21​[Φ−1(u1​),...,Φ−1(un​)]Σ−1⎝⎛​Φ−1(u1​)...Φ−1(un​)​⎠⎞​+21​i=1∑n​(Φ−1(ui​))2}​

Student t Copula函数

  当两个随机变量相互独立时，联合分布可以写成两个边缘分布相乘的形式，即： H ( x , y ) = F ( x ) × G ( y ) H(x,y)=F(x)\times G(y) H(x,y)=F(x)×G(y) 有Sklar定理可得独立Copula的表达式： C ( u , v ) = u × v , u , v ∈ [ 0 , 1 ] 2 C(u,v)=u\times v, u,v\in[0,1]^2 C(u,v)=u×v,u,v∈[0,1]2 独立Copula的散点图如下图：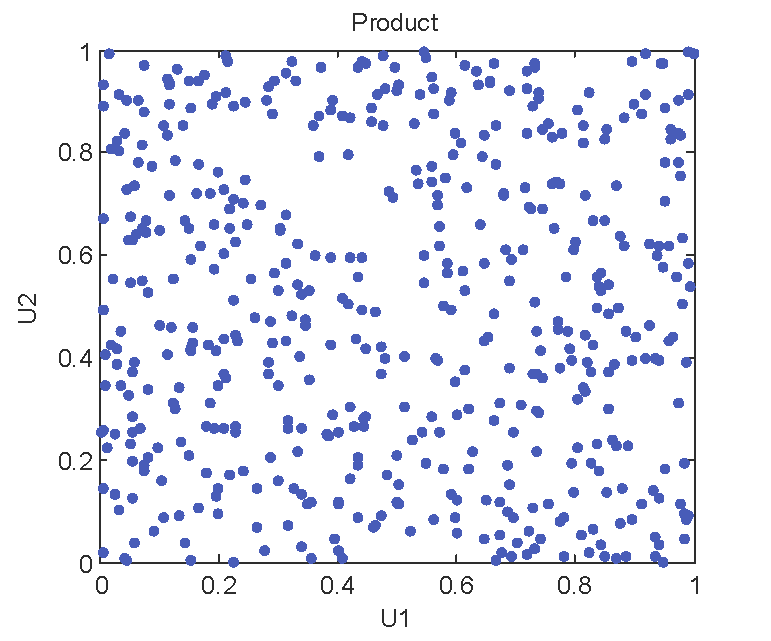

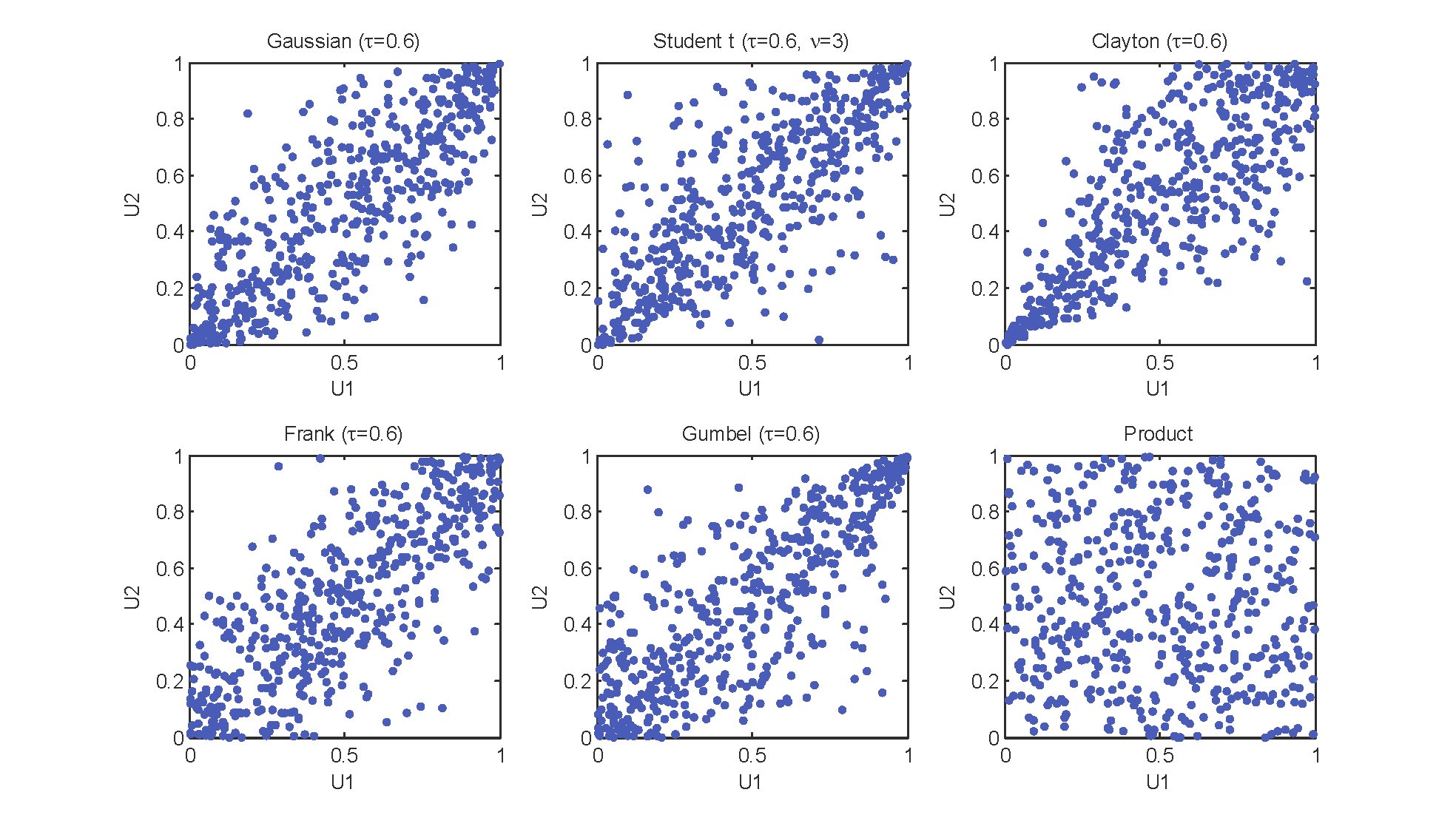
  常见的几种Archimedean Copula及散点图见下。

  参数估计是构建多变量概率模型的重要环节，目前使用较为广泛的参数估计方法主要有相关性指标法、极大似然法、矩估计方法、边际推断法、半参数法等。

  相关性指标法通过Copula函数参数与某个变量相关性指标的关系，先根据样本计算相关性指标，再间接推求Copula函数参数。Gumbel、Clayton和Frank函数的参数可用Kendall秩相关系数进行推求，关系式分别如下：

  若随机变量 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1​,X2​,...,Xn​的联合分布表示为 C ( F X 1 ( x 1 ) , F X 2 ( x 2 ) , . . . , F X n ( x n ) ) C(F_{X_1}(x_1),F_{X_2}(x_2),...,F_{X_n}(x_n)) C(FX1​​(x1​),FX2​​(x2​),...,FXn​​(xn​))， u 1 = F X 1 ( x 1 ) , u 2 = F X 2 ( x 2 ) , . . . , u n = F X n ( x n ) ) u_1=F_{X_1}(x_1),u_2=F_{X_2}(x_2),...,u_n=F_{X_n}(x_n)) u1​=FX1​​(x1​),u2​=FX2​​(x2​),...,un​=FXn​​(xn​))， θ \theta θ为Copula函数的参数，在 ( u 1 , u 2 , . . . , u n ) (u_1,u_2,...,u_n) (u1​,u2​,...,un​)的样本空间上，极大似然函数为： L ( θ ) = ∏ i = 1 n c ( u i 1 , u i 2 , . . . , u i n ; θ ) L(\theta)=\prod_{i=1}^{n}c(u_{i1},u_{i2},...,u_{in};\theta) L(θ)=i=1∏n​c(ui1​,ui2​,...,uin​;θ) 其中 c ( u i 1 , u i 2 , . . . , u i n ; θ ) = ∂ n C ( u i 1 , u i 2 , . . . , u i n ; θ ) ∂ u 1 ∂ u 2 . . . ∂ u n c(u_{i1},u_{i2},...,u_{in};\theta)=\frac{\partial^nC(u_{i1},u_{i2},...,u_{in};\theta)}{\partial u_1\partial u_2...\partial u_n} c(ui1​,ui2​,...,uin​;θ)=∂u1​∂u2​...∂un​∂nC(ui1​,ui2​,...,uin​;θ)​为 n n n维Copula函数的密度函数。

  上式两边取对数，则有： ln ⁡ ( L ( θ ) ) = ∑ i = 1 n ln ⁡ ( c ( u i 1 , u i 2 , . . . , u i n ; θ ) ) ( 3 ) \ln(L(\theta))=\sum_{i=1}^{n}\ln(c(u_{i1},u_{i2},...,u_{in};\theta))\quad\quad(3) ln(L(θ))=i=1∑n​ln(c(ui1​,ui2​,...,uin​;θ))(3) (3)式取得最大值时，必须满足关于参数 θ \theta θ的偏导数为0，即 ∂ ln ⁡ ( L ( θ ) ) ∂ θ = 0 \frac{\partial \ln(L(\theta))}{\partial \theta}=0 ∂θ∂ln(L(θ))​=0

  为了检验所选Copula函数能否准确地表征变量之间的相关性关系，需要对所选的Copula函数进行假设检验。通过确定置信水平下的临界值，与实测数据的统计量进行比较分析，判断所选定的Copula函数是否被接受。非参数Kolmogorov Smimov检验方法，其数学表达式如下。 D = max ⁡ 1 ≤ i ≤ n { ∣ C k − m k n ∣ , ∣ C k − m k − 1 n ∣ } D=\max_{1\leq i\leq n}\left\{\left|C_k-\frac{m_k}{n}\right|,\left|C_k-\frac{m_k-1}{n}\right|\right\} D=1≤i≤nmax​{∣∣∣​Ck​−nmk​​∣∣∣​,∣∣∣∣​Ck​−nmk​−1​∣∣∣∣​} 式中， C k C_k Ck​表示联合观测样本 x k = ( x 1 k , x 2 k , . . . , x n k ) x_k=(x_{1k},x_{2k},...,x_{nk}) xk​=(x1k​,x2k​,...,xnk​)的Copula函数值， m k m_k mk​表示联合观测样本中满足条件 x k ≤ x i k ( i = 1 , 2 , . . . , n ) x_k\leq x_{ik}(i=1,2,...,n) xk​≤xik​(i=1,2,...,n)的联合观测值的个数。

  在利用多种Copula函数对多变量联合分布进行拟合后，需采用拟合优度检验指标进行优选，确定最优拟合Copula函数。

  （1）RMSE准则法

  选取均方根误差准则(RMSE准则)的计算公式如下： R M S E = 1 n ∑ i = 1 n ( p e i − p i ) 2 RMSE=\sqrt{\frac{1}{n}\sum_{i=1}^{n}(pe_i-p_i)^2} RMSE=n1​i=1∑n​(pei​−pi​)2 ​ 式中， p e i pe_i pei​表示经验概率， p i p_i pi​表示理论概率。RMSE值越小，表示拟合效果越好。

  （2）AIC信息准则法

  AIC信息准则包括两个部分，Copula函数拟合的偏差与Copula函数参数个数导致的不稳定性，AIC表达式为： A I C = n ln ⁡ ( M S E ) + 2 m AIC=n \ln(MSE)+2m AIC=nln(MSE)+2m M S E = 1 n ∑ i = 1 n ( p e i − p i ) 2 MSE=\frac{1}{n}\sum_{i=1}^{n}(pe_i-p_i)^2 MSE=n1​i=1∑n​(pei​−pi​)2 式中， m m m为模型参数个数。AIC值越小说明拟合效果越好。

  （3）BIC信息准则法 B I C = n ln ⁡ ( M S E ) + m ln ⁡ n BIC=n\ln(MSE)+m\ln n BIC=nln(MSE)+mlnn BIC值越小，函数拟合效果越好。

  Copula函数应用的前提是随机变量之间具有非线性的相关关系，因此，需要利用变量相关性指标分析特征变量之间的相关性。常用的度量随机变量相关性的统计指标如下：

  （1）Pearson线性相关系数 r r r r = ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 ∑ i = 1 n ( y i − y ˉ ) r=\frac{\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum_{i=1}^{n}(x_i-\bar{x})^2}\sqrt{\sum_{i=1}^{n}(y_i-\bar{y})}} r=∑i=1n​(xi​−xˉ)2 ​∑i=1n​(yi​−yˉ​) ​∑i=1n​(xi​−xˉ)(yi​−yˉ​)​

式中， ( x i , y i ) (x_i,y_i) (xi​,yi​)表示取自总体 ( x , y ) (x,y) (x,y)的样本， i = 1 , 2 , . . . , n i=1,2,...,n i=1,2,...,n； x ˉ \bar{x} xˉ、 y ˉ \bar{y} yˉ​分别表示变量 x x x和 y y y的样本均值。 r r r的取值范围为 [ − 1 , 1 ] [-1,1] [−1,1]，其绝对值越大，表示变量之间的线性相关性越显著。

  （2）Kendall秩相关系数 τ \tau τ

   τ = ( C n 2 ) − 1 ∑ i < j s i g n [ ( x i − x j ) ( y i − y j ) ] \tau=(C_n^2)^{-1}\sum_{i0\\ 0,x=0\\ -1,x00,x=0−1,x