我们通常先针对研究对象抽取出一个合适的数学模型，进而进行分析、综合等探讨。例如，经典控制理论的传递函数，现代控制函数也有自己的模型结构，即状态空间表达式。

1) 状态变量 x(t) ：足以完全表征系统运动状态的最少个数的一组变量。

完全表征：只要给定状态变量的初值 x(t_0) 以及 t\geq t_0 时刻的输入 u(t) ，就能够完全确定系统在任何时间 t\geq t_0 的动态行为。

关于 x(t) 的两点说明：

a. 状态变量是相互独立的

b. 对于一个实际的物理系统，状态变量的个数大于等于系统中独立储能元件的个数

状态向量 x ：若一个系统有 n 个状态变量 x_1(t),x_2(t),...,x_n(t) ,把这 n 个状态变量作为分量所构成的向量就称为系统的状态向量。对同一个动态系统，状态变量的个数是唯一确定的，但是状态向量的选取可以有无穷多种。

2）状态空间：以状态向量的每一个分量 x_1(t),x_2(t),...,x_n(t) 为坐标轴所构成的空间，称为状态空间。

系统任一时刻的状态均可表示为状态空间中的一个点

系统状态随时间变化的过程，在状态空间中描绘出一条轨迹，称为状态轨迹

3）状态方程：由系统状态变量构成的描述系统动态过程的一阶微分方程组，称为系统的状态方程。

状态方程的一般形式为： \dot{x}=Ax+Bu

状态方程用于描述系统输入引起系统状态变化的动态过程

4）输出方程：在指定系统输出y 的情况下，输出向量 y 与状态向量 x 及系统输入向量 u 的函数关系式，称为系统的输出方程。

系统输出方程的一般形式为: y=Cx+Du

系统的状态和输入决定了系统输出的变化

状态方程和输出方程总和起来，构成对一个系统的完整动态描述，称为系统的状态空间表达式。

对于 n 个状态变量、 r 个输入、 m 个输出的动态系统，状态空间表达式的一般形式为：

\dot{x}=Ax+Bu

y=Cx+Du

A\in R (n\times n) ,表征了系统内部状态的联系，称为系统矩阵；

B\in R (n\times r) ,表征了输入对状态的作用，称为输入矩阵，也称为控制矩阵；

C\in R (m\times n) ,表征了输出与状态变量的关系，称为输出矩阵；

D\in R (m\times r) ,表征了输出与输入的关系，称为直接传输矩阵。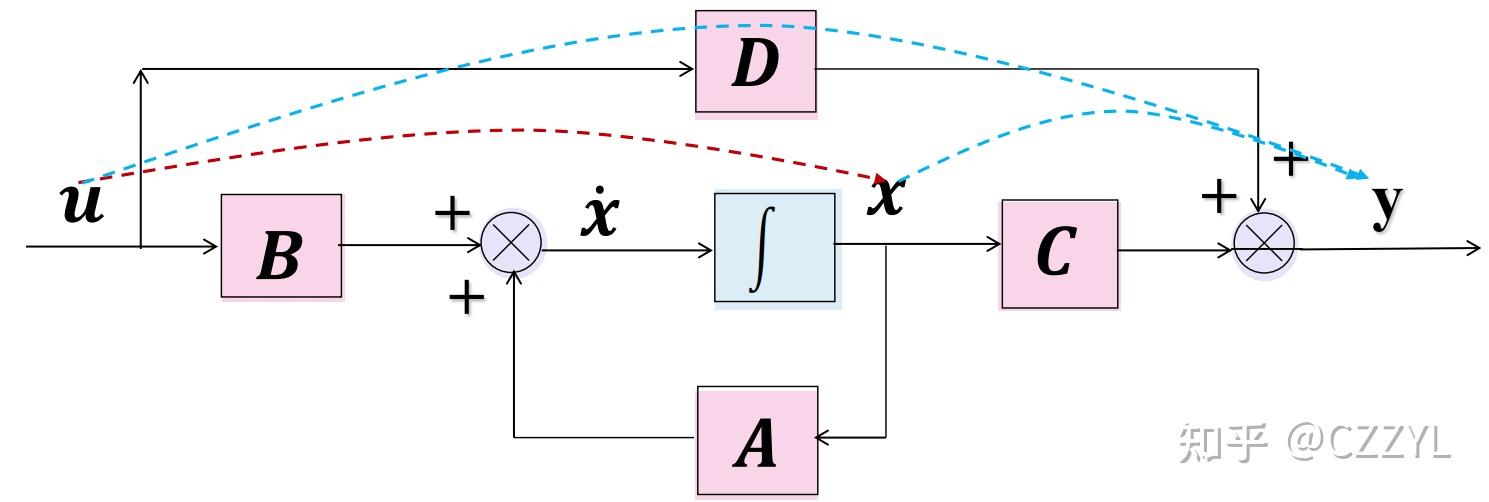

显然，状态空间表达式的方框图，只含有比例、积分、加法三类基本环节。

主要有三种：方框图、机理法、传函转化或高阶微分方程实现

1）由方框图列写

例：根据系统模拟结构图，建立其状态空间表达式

步骤：a.传递函数变换 b.选取状态变量 c.列写状态方程

a.传递函数变换

b.选取状态变量

每个积分器的输出选做一个状态变量，共6个状态变量：

x1,x2,...,x6

c.列写状态方程

状态空间表达式：

状态方程：

输出方程：

2）从系统的基本原理进行推导（机理法从略）

3）根据传递函数或高阶微分方程实现

实现方法：能控标准型实现、能观标准型实现、特征值规范型实现（对角规范型实现、约当规范型实现）

实现存在的条件： m\leq n

两个特性：a.实现具备非唯一性 b.没有零极点对消的传递函数的实现称为最小实现

例：

已知系统的传递函数为：

g(s)=(s+3)/(s^2+3s+2)

写出上式的能控规范型、能观规范型、特征值规范型的状态空间表达式。

a）中间变量法：

由题可得： Y(s)=(s+3)/(s^2+3s+2)U(s)

设 \hat Y(s)=1/(s^2+3s+2)U(s)

则有： Y(s)=(s+3)\hat Y(s) , (s^2+3s+2)\hat Y(s)=U(s)

对上两式取拉氏反变换可得： y= \dot {\hat{y} }+ \hat{y}, \dot {\dot {\hat{y} }}+3\dot {\hat{y} }+ 2\hat{y} =u

取状态变量： [x_1 , x_2]^T=[\hat{y} , \dot {\hat{y} } ]^T

则有：

写成矩阵的形式：

b）待定系数法：

取状态变量：

由

解得

系统的状态空间表达式为：

c）特征值规范型法：

系统的特征多项式为: \lambda^2+3\lambda+2=0 解得： \lambda_1=-1,\lambda_2=-2

由系统的传递函数可得：

Y(s)=(s+3)/[(s+1)(s+2)]U(s)=2/(s+1)U(s)-1/(s+2)U(s)

取状态变量的拉氏变换为：

X_1(s)=1/(s+1)U(s)

X_2(s)=1/(s+2)U(s)

取拉氏反变换可得：

\dot x_1=-x_1 +u

\dot x_2=-2x_2 +u

y=2x_1 -x_2

则有系统的状态空间表达式为：

状态空间表达式如下:

\dot{x}=Ax+Bu

y=Cx+Du

令， z=T^{-1}x （线性变换）

则有:

\dot{z}=T^{-1}ATz+T^{-1}Bu

y=CTz+Du

x(0)=x_0,z(0)=T^{-1}x(0)

注：

a. 同一系统不同状态向量之间必然存在一种线性变换的关系

b. 非奇异线性变换不改变系统的特征值

1）对角规范型

对系统 \dot{x}=Ax+Bu 进行线性变换： z=T^{-1}x ，必可化为对角规范型。

其中，变换阵为特征向量组成 T=[p_1,p_2,...p_n]

2）约当规范型（系统存在重根）

代数重数：设 \lambda_i 为系统矩阵A的特征值,若 \lambda_i 的重根数为 \sigma_i ，则称 \lambda_i 的代数重数为 \sigma_i

几何重数：设V为n维线性空间， \lambda_i 为系统矩阵A的特征值，则 \lambda_i 的特征子空间

V_{\lambda_i}=p_i\in V|Ap_i+\lambda_ip_i 的维数 \alpha_i , 称为 \lambda_i 特征值的几何重数。

此外，有

\alpha_i=n-rank(\lambda_iI-A)

对给定系统 \dot{x}=Ax+Bu 进行线性变换 z=T^{-1}x ，化为约当规范型的矩阵 T 如何求解

步骤：

a.求解特征根 |\lambda_iI-A|=0

b.求几何重数 \sigma_i

c.求每一特征值对应特征向量 \lambda_2p_2-Ap_2=-p_1

d.求系数矩阵 \hat A=T^{-1}AT,\hat B=T^{-1}B

\dot{x}=Ax+Bu

y=Cx+Du

得传递函数： Y（s）=(C(sI-A)^{-1}B+D)U(s)

x(k+1)=Gx(k)+Hu(k)

y(k)=Cx(k)+Du(k)

\dot{x}=A(t)x+B(t)u

y=C(t)x+D(t)u

1）非线性时变系统

\dot{x}=f(x,u,t)

y=g(x,u,t)

式中，f，g为函数向量；

2）非线性定常系统

\dot{x}=f(x,u)

y=g(x,u)