AR、MA、ARMA和ARIMA模型

您所在的位置：网站首页 › ar和arch › AR、MA、ARMA和ARIMA模型

AR、MA、ARMA和ARIMA模型

#AR、MA、ARMA和ARIMA模型| 来源: 网络整理| 查看: 265

ARMA模型的全称是自回归移动平均模型，它是目前最常用的拟合平稳序列的模型。它又可以细分为AR模型、MA模型和ARMA三大类。都可以看做是多元线性回归模型。

AR模型

具有如下结构的模型称为 $p$ 阶自回归模型，简记为 $AR(p)$ 。

$x_t=\phi _0+\phi _1x_{t-1}+\phi _2x_{t-1}+...+\phi _px_{t-p}+\varepsilon _t$

即在t时刻的随机变量 $X_t$ 的取值 $x_t$ 是前 $p$ 期 $x_{t-1},x_{t-1},..,x_{t-p}$ 的多元线性回归，认为 $x_t$ 主要是受过去 $p$ 期的序列值的影响。误差项是当期的随机干扰 $\varepsilon _t$ ，为零均值白噪声序列，

平稳AR模型的性质如下所示：

1）均值

对满足平稳性条件的 $AR(p)$ 模型的方程，两遍取期望，得：

已知 $E(x_t)=\mu ,E(\varepsilon _t)=0$ ，所以： $\mu =\phi _0+\phi _1\mu +\phi _2\mu +...+\phi _p\mu$ ，解得：

注意：因为之前已经定义了平稳性序列的均值为常数，所以 $E(x_t)=E(x_{t-1})=...=E(x_{t-p})$

2）方差

平稳 $AR(p)$ 模型的方差有界，等于常数。

3）自相关系数(ACF)

平稳 $AR(p)$ 模型的自相关系数 $\rho _k=\rho (t,t-k)=\frac{cov(X_t,X_{t-k})}{\sigma _t\sigma _{t-k}}$ 呈指数的速度衰减，始终有非零取值，不会在k大于某个常数之后就恒等于零，这个性质就是平稳 $AR(p)$ 模型的自相关系数 $\rho _k$ 具有拖尾性。

4）偏自相关系数(PACF)

对于一个平稳 $AR(p)$ 模型，求出延迟k期自相关系数 $\rho _k$ 时，实际上得到的并不是 $X_t$ 与 $X_{t-k}$ 之间单纯的相关关系，因为 $X_t$ 同时还会受到中间k-1个随机变量 $X_{t-1},X_{t-2},...,X_{t-k}$ 的影响，所以自相关系数 $\rho _k$ 里面实际上掺杂了其他变量对 $X_t$ 与 $X_{t-k}$ 的相关影响，为了单纯的预测 $X_{t-k}$ 对 $X_t$ 的影响，引进偏自相关系数的概念。

MA模型

具有如下结构的模型称为 $q$ 阶自回归模型，简记为 $MA(q)$ 。

$x_t=\mu +\varepsilon _t-\theta _1\varepsilon _{t-1}-\theta _2\varepsilon _{t-2}-...-\theta _q\varepsilon _{t-q}$

即在t时刻的随机变量 $X_t$ 的取值 $x_t$ 是前 $q$ 期的随机扰动 $\varepsilon _{t-1},\varepsilon _{t-2},...,\varepsilon _{t-q}$ 的多元线性函数，误差项是当期的随机干扰 $\varepsilon _t$ ，为零均值白噪声序列， $\mu$ 是序列 $\{X_t\}$ 的均值。认为 $x_t$ 主要是受过去 $q$ 期的误差项的影响。

平稳 $MA(q)$ 模型的性质如下：

ARMA模型

具有如下结构的模型称为自回归移动平均模型，简记为 $ARMA(p,q)$ 。

$x_t=\phi _0+\phi _1x_{t-1}+\phi _2x_{t-1}+...+\phi _px_{t-p}+\varepsilon _t-\theta _1\varepsilon _{t-1}-\theta _2\varepsilon _{t-2}-...-\theta _q\varepsilon _{t-q}$

即在t时刻的随机变量 $X_t$ 的取值 $x_t$ 是 $p$ 期 $x_{t-1},x_{t-1},..,x_{t-p}$ 和前 $q$ 期的随机扰动 $\varepsilon _{t-1},\varepsilon _{t-2},...,\varepsilon _{t-q}$ 的多元线性函数，误差项是当前的随机干扰 $\varepsilon _t$ ，为零均值白噪声序列。认为 $x_t$ 主要是受过去 $p$ 期的序列值和过去 $q$ 期的误差项的共同影响。

特别的，当 $q$ =0时，是 $AR(p)$ 模型；当 $p$ =0时，是 $MA(q)$ 模型。

平稳 $ARMA(p,q)$ 的性质

平稳时间序列建模

某个时间序列经过预处理，被判定为平稳非白噪声序列，就可以利用ARMA模型进行建模，计算出平稳非白噪声序列 $\{X_t\}$ 的自相关系数和偏自相关系数，再由 $AR(p)$ 模型、 $MA(q)$ 模型和 $ARMA(p,q)$ 的自相关系数和偏自相关系数的性质，选择合适的模型。建模步骤如下：

非平稳性时间序列分析

实际上，在自然界中绝大部分序列都是非平稳的，因而对非平稳序列的分析更为普遍、更为重要，创造出来的分析方法也更多。

对非平稳时间序列的分析方法可以分为确定性因素分解的时序分析和随机时序分析两大类。

确定性因素分解的方法把所有序列的变化都归结为4个因素(长期趋势、季节变动、循环变动和随机波动)的综合影响，其中长期趋势和季节变动的规律性信息通常比较容易提取，而由随机因素导致的波动则非常难确定和分析，对随机信息浪费严重，会导致模型拟合精度不够理想。

随机时序分析法的发展就是为了弥补确定性因素分解方法的不足。根据时间序列的不同特点，随机时序可以建立的模型有ARIMA模型、残差自回归模型、季节模型、异方法模型等。这里主要介绍ARIMA模型。

1. 差分运算

(1) $p$ 阶差分

相距一期的两个序列值之间的减法运算称为1阶差分运算

(2) $k$ 步差分

相距 $k$ 期的两个序列值之间的减法运算称为 $k$ 步差分运算

2. ARIMA模型

差分运算具有强大的确定性信息提取能力，许多非平稳序列差分后会显示出平稳序列的性质，这时称这个非平稳序列为差分平稳序列。对差分平稳序列可以使用ARMA模型进行拟合。ARIMA模型的实质就是差分运算与ARMA模型的组合。以下为建模步骤：

示例

对某餐厅2015/1/1~2015/2/6某餐厅的销售数据进行建模。

1）检验序列的平稳性

明显可以看到在第一幅时序图中该序列有明显的单调递增趋势，可以判断为使非平稳序列，第二幅自相关图中显示自相关系数长期大于零，说明序列间具有很强的长期相关性；在第三幅图中是单位根检验表，其中p值显著大于0.05，最终判断该序列为非平稳序列（非平稳序列一定不是白噪声序列）。

2）对原始序列进行一阶差分，并进行平稳性和白噪声检验

首先差分之后对其进行平稳性检验，过程同上

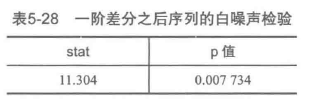
经过一阶差分之后的序列的时序图在均值附近比较平稳的波动、自相关图有很强的短期相关性、单位根检验p值小于0.05，所以一阶差分之后的序列是平稳序列。

接下来对一阶差分后的序列做白噪声检验：

输出的p值远小于0.05，所以一阶差分之后的序列是平稳的非白噪声序列。

3）对一阶差分之后的平稳非白噪声序列拟合ARMA模型，就是确定p值和q值。

第一种方法：认为识别的方法

一阶差分后自相关图显示出1阶截尾，所以可以考虑用MA(1)模拟一阶差分后的序列，即对原始序列建立ARIMA(0,1,1)模型。

第二种方法：相对最优模型识别

计算ARMA(p,q)。当p和q均小于等于3的所有组合的BIC信息量，取其中BIC信息量达到最小的模型阶数。

ARIMA模型实现代码：

def programmer_6(): """ 警告解释： # UserWarning: matplotlib is currently using a non-GUI backend, so cannot show the figure "matplotlib is currently using a non-GUI backend, " 调用了多次plt.show() 解决方案，使用plt.subplot() # RuntimeWarning: overflow encountered in exp 运算精度不够 forecastnum-->预测天数 plot_acf().show()-->自相关图 plot_pacf().show()-->偏自相关图 """ discfile = 'data/arima_data.xls' forecastnum = 5 data = pd.read_excel(discfile, index_col=0) fig = plt.figure(figsize=(8, 6)) # 第一幅自相关图 ax1 = plt.subplot(411) fig = plot_acf(data, ax=ax1) # 平稳性检测 print(u'原始序列的ADF检验结果为：', ADF(data[u'销量'])) # 返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore # 差分后的结果 D_data = data.diff().dropna() D_data.columns = [u'销量差分'] # 时序图 D_data.plot() plt.show() # 第二幅自相关图 fig = plt.figure(figsize=(8, 6)) ax2 = plt.subplot(412) fig = plot_acf(D_data, ax=ax2) # 偏自相关图 ax3 = plt.subplot(414) fig = plot_pacf(D_data, ax=ax3) plt.show() fig.clf() print(u'差分序列的ADF检验结果为：', ADF(D_data[u'销量差分'])) # 平稳性检测 # 白噪声检验 print(u'差分序列的白噪声检验结果为：', acorr_ljungbox(D_data, lags=1)) # 返回统计量和p值 data[u'销量'] = data[u'销量'].astype(float) # 定阶 pmax = int(len(D_data) / 10) # 一般阶数不超过length/10 qmax = int(len(D_data) / 10) # 一般阶数不超过length/10 bic_matrix = [] # bic矩阵 data.dropna(inplace=True) # 存在部分报错，所以用try来跳过报错；存在warning，暂未解决使用warnings跳过 import warnings warnings.filterwarnings('error') for p in range(pmax + 1): tmp = [] for q in range(qmax + 1): try: tmp.append(ARIMA(data, (p, 1, q)).fit().bic) except: tmp.append(None) bic_matrix.append(tmp) # 从中可以找出最小值 bic_matrix = pd.DataFrame(bic_matrix) # 用stack展平，然后用idxmin找出最小值位置。 p, q = bic_matrix.stack().astype(float).idxmin() print(u'BIC最小的p值和q值为：%s、%s' % (p, q)) #print("data",data) X = data.values print(X) history = [x for x in X] model = ARIMA(history, order=(0, 1, 1)).fit() # 建立ARIMA(0, 1, 1)模型 model.summary2() # 给出一份模型报告 print("5天的预测",model.forecast(forecastnum)) # 作为期5天的预测，返回预测结果、标准误差、置信区间。 if __name__ == "__main__": programmer_6()

数据可到链接: https://pan.baidu.com/s/1ap0ZuXyVRNls3GFGD6Xo8A 提取码: 7pe9下载

参考书目《Python数据分析与挖掘实战》

【本文地址】

AR、MA、ARMA和ARIMA模型

AR、MA、ARMA和ARIMA模型

今日新闻

推荐新闻