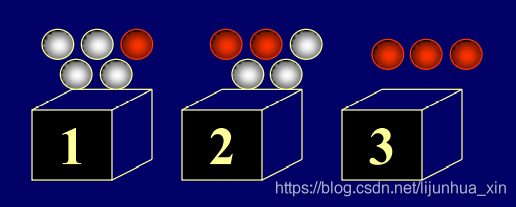
本文仅用于记录自己的学习过程！若有不对之处欢迎批评指正。

按字面意思理解，即事件A在事件B已经发生的情况下发生的概率。记作 P ( A ∣ B ) P(A|B) P(A∣B). 给出条件概率的一般定义： 设 A 与 B 是 两 个 事 件 ， 且 P ( B ) > 0 ， 称 ： P ( A ∣ B ) = P ( A B ) P ( B ) 设A与B是两个事件，且P(B)>0，称：\\P(A|B)=\frac{P(AB)} {P(B)} 设A与B是两个事件，且P(B)>0，称：P(A∣B)=P(B)P(AB)​ 因为条件概率满足概率的标准化定义，因此在一中所说的六条性质对于条件概率同样成立。 举个例子，比如原来有 P ( A ) = 1 − P ( A ‾ ) P(A)=1-P(\overline A) P(A)=1−P(A),则如今有 P ( A ∣ B ) = 1 − P ( A ‾ ∣ B ) P(A|B)=1-P(\overline{A}|B) P(A∣B)=1−P(A∣B) 由上述定义，可以很自然的引出乘法公式。 若 P ( A ) > 0 ， 则 有 P ( A B ) = P ( A ) P ( B ∣ A ) 若 P ( B ) > 0 ， 则 有 P ( A B ) = P ( B ) P ( A ∣ B ) 若P(A)>0，则有P(AB)=P(A)P(B|A)\\ 若P(B)>0，则有P(AB)=P(B)P(A|B) 若P(A)>0，则有P(AB)=P(A)P(B∣A)若P(B)>0，则有P(AB)=P(B)P(A∣B) 要记忆的话也比较容易，谁大于0，谁就出现的次数多。 关于这个P(A)>0的理解：A、B可能为互斥事件，这时当A或B中一个发生时，另外一个概率就为0了。 乘法公式还是比较重要的。并且其可以拓展至无限项，这边给出三项的乘法公式： P ( A B C ) = P ( C ∣ A B ) P ( B ∣ A ) P ( A ) P(ABC)=P(C|AB)P(B|A)P(A) P(ABC)=P(C∣AB)P(B∣A)P(A)

例1：有三个箱子,分别编号为1,2,3. 1号箱装有1个红 球4个白球, 2号箱装有2红3白球 , 3号箱装有3 红球. 某人从三箱中任取一箱,从中任意摸出一球, 求取得 红球的概率.

记A={摸到红球}, B i B_i Bi​ ={在第i个箱子里摸球}， 按照条件概率的定义，红球可在1,2,3中都摸到，列式 P ( A ) = P ( A ∣ B 1 ) + P ( A ∣ B 2 ) + P ( A ∣ B 3 ) P(A)=P(A|B_1)+P(A|B_2)+P(A|B_3) P(A)=P(A∣B1​)+P(A∣B2​)+P(A∣B3​), 解释一下就是：在1中摸到球的概率+在2中摸到球的概率+在3中摸到球的概率，这样你就写出了一个全概率公式。 总结一下全概率公式，给出一般式： P ( A ) = ∑ i = 1 n P ( B i ) P ( A ∣ B i ) P(A)=\sum_{i=1}^{n}P(B_i)P(A|B_i) P(A)=i=1∑n​P(Bi​)P(A∣Bi​)

设 B 1 , B 2 , B 3 … B n 是 样 本 空 间 S 的 一 个 划 分 ， A 为 S 中 的 任 何 一 个 事 件 ， 且 P ( A ) > 0 , 则 有 ： 设B_1,B_2,B_3…B_n是样本空间S的一个划分，A为S中的任何一个事件，且P(A)>0,则有： 设B1​,B2​,B3​…Bn​是样本空间S的一个划分，A为S中的任何一个事件，且P(A)>0,则有： P ( B i ∣ A ) = P ( A B i ) P ( A ) = P ( B i ) P ( A ∣ B i ) ∑ k = 1 n P ( B k ) P ( A ∣ B k ) , i = 1 , 2 , 3... n P(B_i|A)=\frac {P(AB_i)} {P(A)}=\frac {P(B_i)P(A|B_i)} {\sum_{k=1}^{n}P(B_k)P(A|B_k)},i=1,2,3...n P(Bi​∣A)=P(A)P(ABi​)​=∑k=1n​P(Bk​)P(A∣Bk​)P(Bi​)P(A∣Bi​)​,i=1,2,3...n 说明一下： 第一个等号后面，其本质就是条件概率的变式，然后分别把P(A|B_i)用乘法公式展开，把P(A)用全概率公式展开。之后会有一个例题来熟悉一下贝叶斯公式。 特别要注意的是：贝叶斯公式的应用场景是先知道结论，比如已知摸出红球，问从某个盒子里摸出的概率（例一变种）

只需记住这一条定律即可： A 、 B 两 事 件 独 立 的 充 要 条 件 是 ： P ( A B ) = P ( A ) P ( B ) A、B两事件独立的充要条件是：\\P(AB)=P(A)P(B) A、B两事件独立的充要条件是：P(AB)=P(A)P(B) 几个的注意点： 1、若A、B相互独立，则 A 与 B ‾ , A ‾ 与 B ， A ‾ 与 B ‾ ， 也 相 互 独 立 A与\overline{B},\overline{A}与B，\overline{A}与\overline{B}，也相互独立 A与B,A与B，A与B，也相互独立 2、该定律可拓 n n n个事件，下面给出三个事件的相互独立公式(需同时满足下列4个式子)： P ( A B ) = P ( A ) P ( B ) P ( A C ) = P ( A ) P ( C ) P ( B C ) = P ( B ) P ( C ) P ( A B C ) = P ( A ) P ( B ) P ( C ) P(AB)=P(A)P(B)\\ P(AC)=P(A)P(C)\\ P(BC)=P(B)P(C)\\ P(ABC)=P(A)P(B)P(C) P(AB)=P(A)P(B)P(AC)=P(A)P(C)P(BC)=P(B)P(C)P(ABC)=P(A)P(B)P(C)

在 n n n次重复实验中，设 P ( A ) = k P(A)=k P(A)=k,事件A发生 k k k次的概率为： P n ( k ) = ∁ n k p k ( 1 − p ) k P_n(k)=\complement_n^kp^k(1-p)^k Pn​(k)=∁nk​pk(1−p)k 高中公式，没啥好说的，不理解记住就好。

稍微解释一下吧： 分析一下题干，抓住重点结果发现向上的一面全是国徽，看到“结果”二字，马上想到这是利用贝叶斯公式。那在本题中所谓的样本空间划分就是“取到正品”和“取到废品”，实在无法理解的话就理解成在一个装满正品的箱子和一个装满废品的箱子中摸硬币，但是摸到废品箱子的概率是 b a + b \frac{b}{a+b} a+bb​,摸到正品的概率是 a a + b \frac{a}{a+b} a+ba​然后套公式就完事了。

这篇主要讲了条件概率，其实贝叶斯公式就是条件概率的一种形式嘛。至于独立性，比较简单。虽然一般来说事件是否独立题目不会明说，但是靠常识就能分清。比如两颗种子，1号种子发芽与否会影响到2号种子吗？显然不会的嘛！