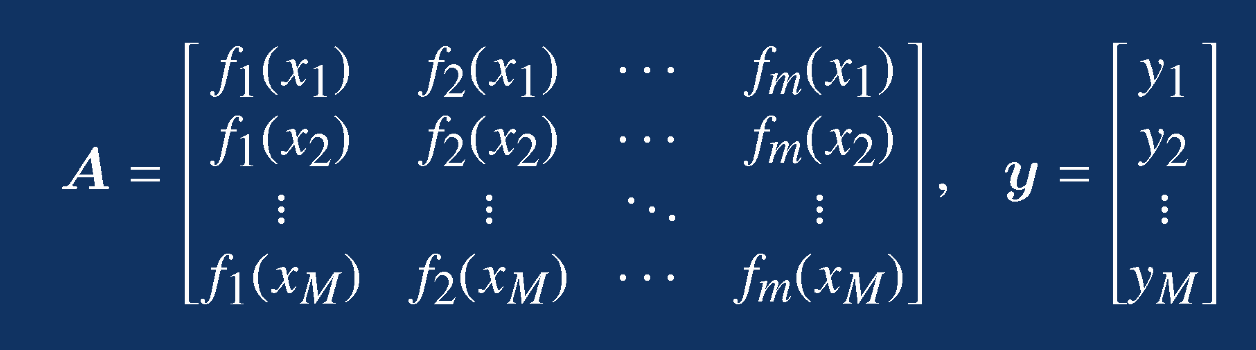基于MATLAB解决数据拟合的振荡现象（附完整代码与算法）

您所在的位置：网站首页 › MATLAB怎么拟合多项式 › 基于MATLAB解决数据拟合的振荡现象（附完整代码与算法）

基于MATLAB解决数据拟合的振荡现象（附完整代码与算法）

2024-07-14 07:00| 来源: 网络整理| 查看: 265

前言

用插值的方法对数据进行近似时，要求所得到的插值多项式经过已知节点。在数据点比较多的情况下，插值多项式往往是高次多项式，这时就很容易出现振荡现象，也称之为龙格现象。这种现象虽然在插值节点上没有误差，但是在插值节点之外插值误差变得很大，从整体上看，插值逼近的效果就变得很差。

由此我们需要利用数据拟合方法，数据拟合就是求一个简单的函数或多项式，例如是一个低次多项式，不要求一定得通过已知的这些点，而要求在整体上尽量好的逼近原函数。这时，在每个已知点上就会有误差。数据拟合就是从整体上使误差尽量小一些。

一. 多项式拟合

n次多项式的表达式如下：

$g(x)=c_1x^n+c_2x^{n-1}+\cdots+c_{n+1}$

给定L个数据，曲线与数据点 $(x_i,y_i)$ 的残差可计算如下：

$r_i=y_i-g(x_i),\quad i=1,2,\cdots,L$

残差的平方和R可计算为如下： $R=\sum_{i=1}^L r_i^2$

进一步化简R可得：

$R=(y_i-\sum_{i=1}^nc_ix^{n+1-i})^2$

根据函数的知识铺垫，为了使R最小化，只需要R关于 $c_j$ 的偏导数为0即可，如下：

$\frac{\partial R}{\partial c_j}=0,\quad j=1,2,\cdots,n+1$

进一步化简可得：

$\sum_{j=1}^{n+1}(\sum_{i=1}^Lx_i^{2n+2-j-k})c_j=\sum_{i=1}^Lx_i^{n+1-k}y_i,\quad k=1,2,\cdots,n+1$

将上述形式写成矩阵可得如下：

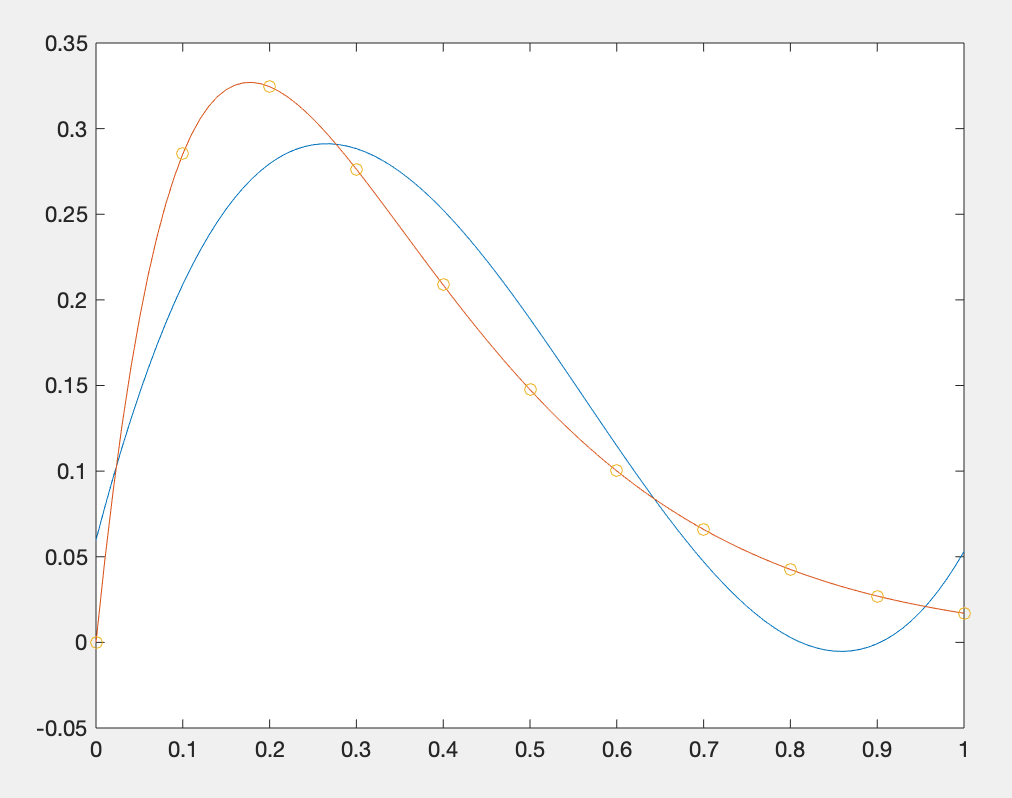
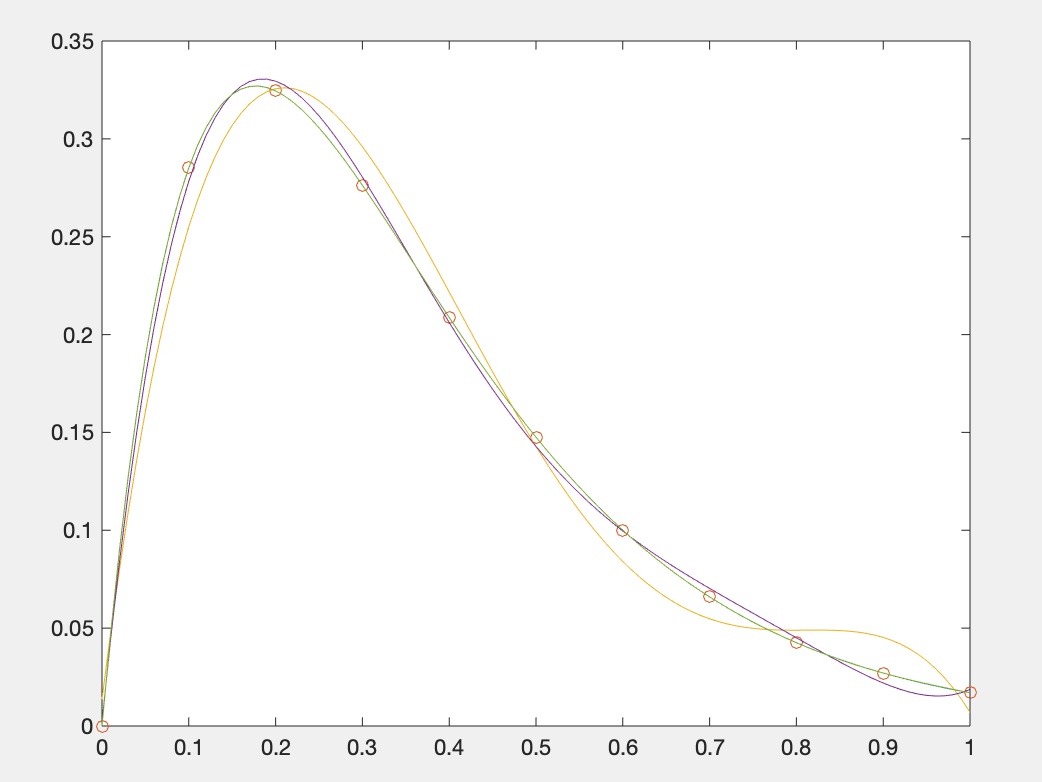
在MATLAB中，多项式拟合命令格式如下：

p=polyfit(x,y,n) %x和y为原始的样本点构成的向量 %n为选定的多项式阶次 %p为多项式系数按降幂排列得出的行向量例题1

自行选择一些来自f(x)的数据点，用多项式拟合的方法在3、4、5、8不同阶次下进行拟合。

$f(x)=(x^2-3x+5)e^{-5x}sinx$

解：

MATLAB代码如下：

%拟合该数据的3次多项式 x0=0:.1:1; y0=(x0.^2-3*x0+5).*exp(-5*x0).*sin(x0); p3=polyfit(x0,y0,3); vpa(poly2sym(p3),10) %显示该多项式 %绘制拟合曲线 x=0:0.01:1; y_normal=(x.^2-3*x+5).*exp(-5*x).*sin(x); y1=polyval(p3,x); %拟合数据结果 plot(x,y1,x,y_normal,x0,y0,'o') %两条线，一组离散点 %4次、5次、8次进行拟合 p4=polyfit(x0,y0,4);y2=polyval(p4,x); p5=polyfit(x0,y0,5);y3=polyval(p5,x); p8=polyfit(x0,y0,8);y4=polyval(p8,x); figure; %第二张图 plot(x,y_normal,x0,y0,'o',x,y2,x,y3,x,y4) %四条线，一组离散点

运行结果：

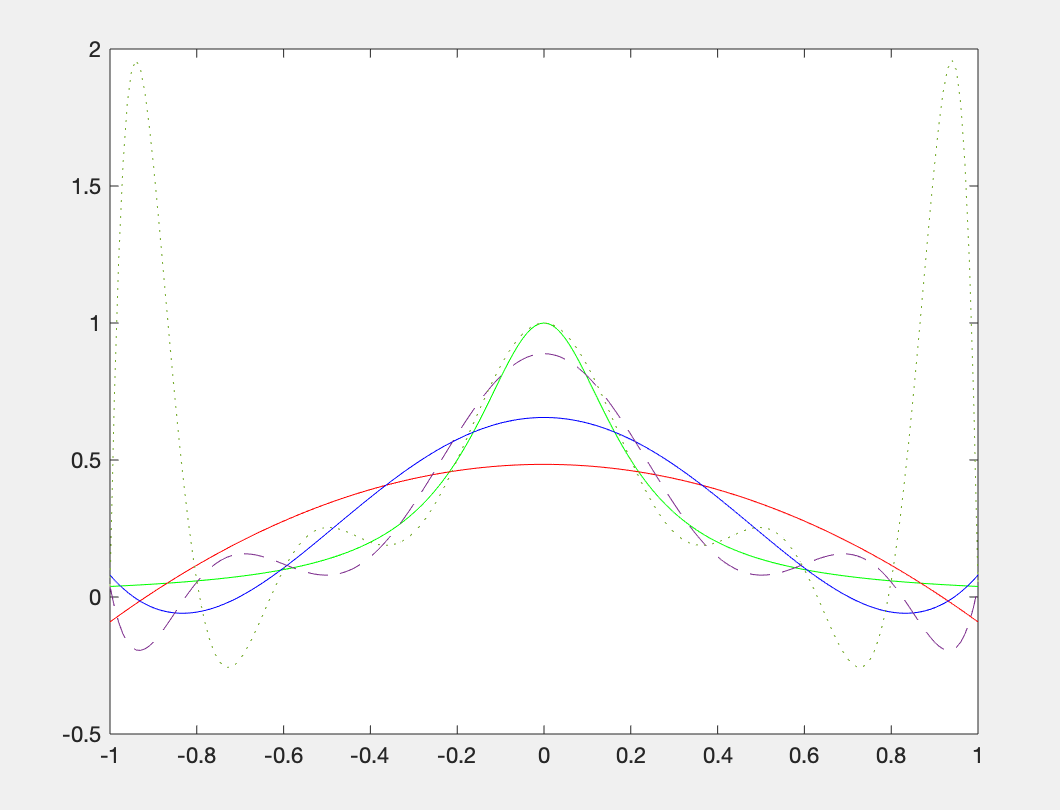
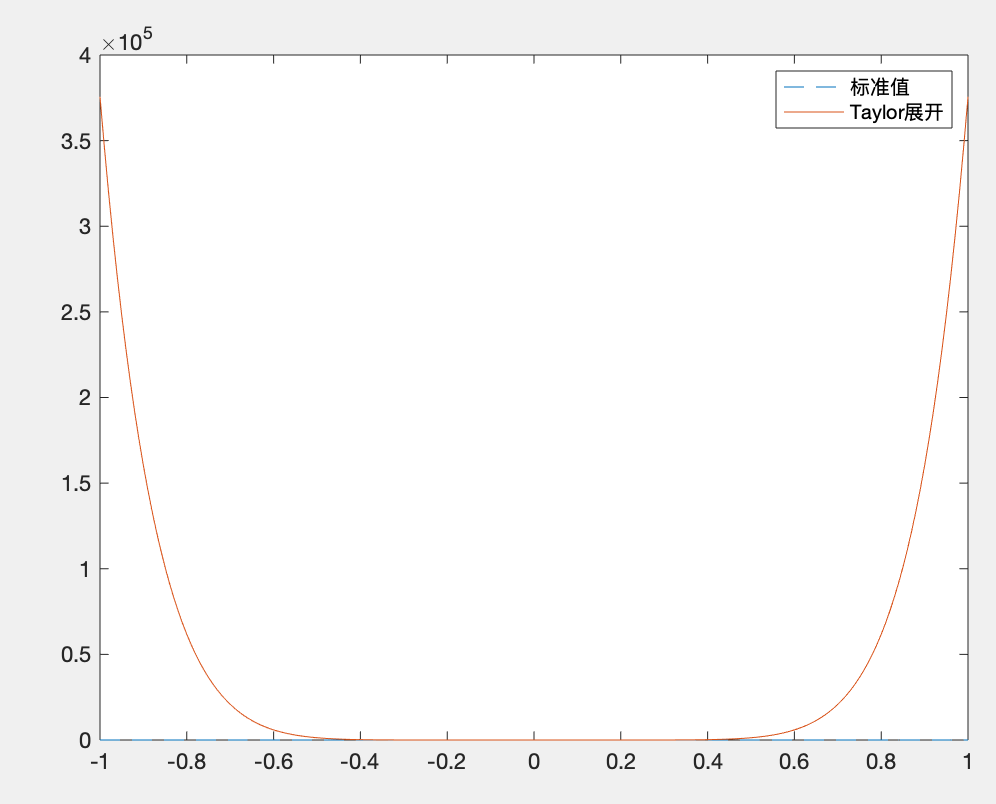
例题2

对f(x)进行3次、5次、8次、10次多项式拟合，并分析Taylor幂级数的展开效果。

$f(x)=\frac{1}{1+25x^2},\quad -1\leq x\leq1$

解：

MATLAB代码如下：

clc;clear; %多项式拟合 x0=-1+2*[0:10]/10; y0=1./(1+25*x0.^2); %生成样本点） x=-1:.01:1; ya=1./(1+25*x.^2); %标准点 p3=polyfit(x0,y0,3); y1=polyval(p3,x); p5=polyfit(x0,y0,5); y2=polyval(p5,x); p8=polyfit(x0,y0,8); y3=polyval(p8,x); p10=polyfit(x0,y0,10); y4=polyval(p10,x); %绿色线为标准值，红色线为3次拟合，蓝色线为5次拟合，分段线为8次拟合，点线为10次拟合 plot(x,ya,'g',x,y1,'r',x,y2,'b',x,y3,'--',x,y4,':') %Taylor幂级数展开 syms X; Y=1/(1+25*X^2); P=taylor(Y,X,'order',10); %展开 %画图 X1=-1:0.01:1; Ya=1./(1+25*X1.^2); Y1=subs(P,X,X1); figure; plot(X1,Ya,'--',X1,Y1) legend('标准值','Taylor展开')

运行结果：

对结果的分析：此例题中不论是多项式拟合，还是Taylor展开的结果，都不太精确。

二. 函数线性组合的曲线拟合

给定某函数的线性组合，如下：

$g(x)=c_1f_1 (x)+c_2f_2 (x)+\cdots+c_nf_n (x)$

上式子中 $f_1(x),f_2(x),\cdots,f_n(x)$ 均为已知函数， $c_1,c_2,\cdots,c_n$ 为待定系数。

如果已经测出了M组数据：

$(x_1,y_1),(x_2,y_2),\cdots,(x_M,y_M)$

则可以建立如下线性方程组：

$Ac=y$

上式子中的c理解为 $c=[c_1,c_2,\cdots,c_n]^T$ ，且矩阵A和y理解为如下：

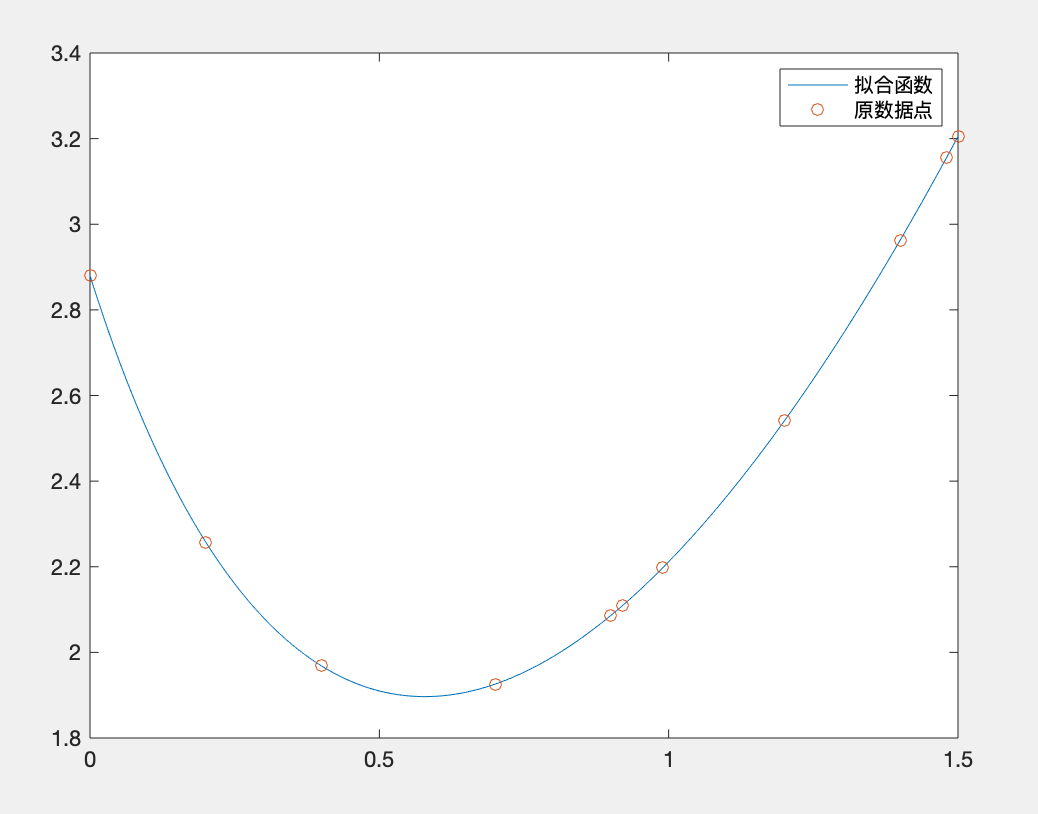
由此，该方程的最小二乘解为：

c=A\y

例题3

假设测出一组数据 $(x_i,y_i)$ 如下表，且函数原模型y(x)已给定，用已知数据求出待定系数 $c_i$ 的值。

$y(x)=c_1+c_2e^{-3x}+c_3cos(-2x)e^{-4x}+c_4x^2$

$x_i$ 00.20.40.70.90.920.991.21.41.481.5 $y_i$ 2.882.25761.96831.92582.08622.1092.19792.54092.96273.1553.2052

解：

MATLAB代码如下：

clc;clear; %计算系数 x=[0 0.2 0.4 0.7 0.9 0.92 0.99 1.2 1.4 1.48 1.5]'; y=[2.88 2.2576 1.9683 1.9258 2.0862 2.109 2.1979... 2.5409 2.9627 3.155 3.2052]'; A=[ones(size(x)),exp(-3*x),cos(-2*x).*exp(-4*x),x.^2]; c=A\y %图形显示 x0=[0:0.01:1.5]'; A1=[ones(size(x0)),exp(-3*x0),cos(-2*x0).*exp(-4*x0),x0.^2]; y1=A1*c; plot(x0,y1,x,y,'o') legend('拟合函数','原数据点')

运行结果：

例题4

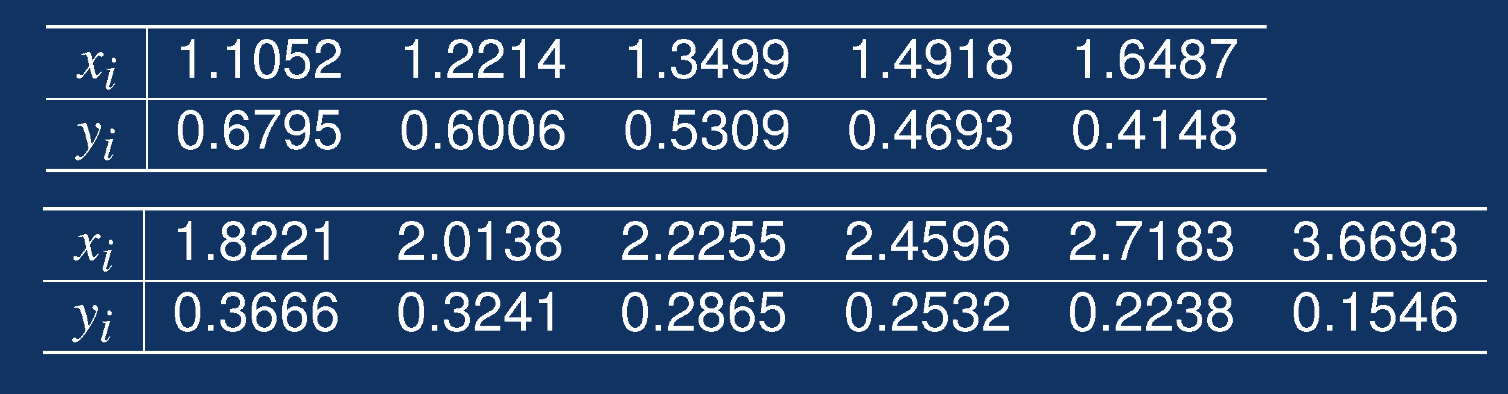
假设测出一组实际数据，对其进行函数拟合。

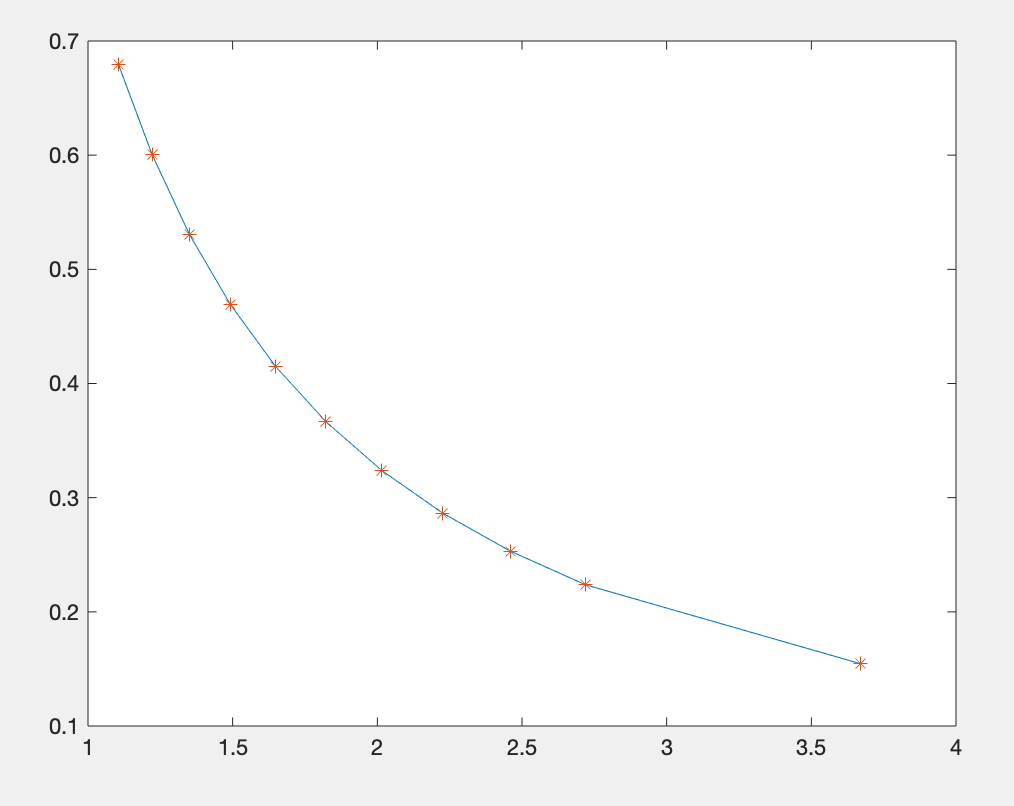
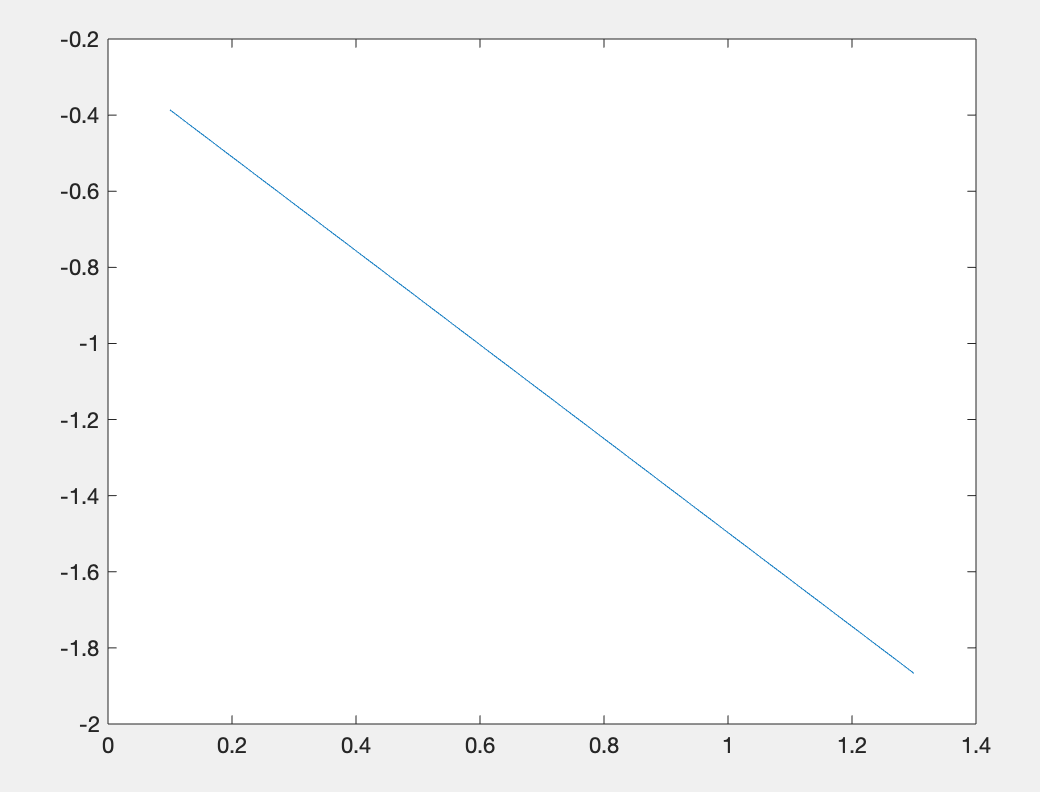
解：

第一步：对给定数据进行分析

MATLAB代码如下：

clc;clear; %数据分析 x=[1.1052 1.2214 1.3499 1.4918 1.6487 1.8221 2.0138 2.2255... 2.4596 2.7183 3.6693]; y=[0.6795 0.6006 0.5309 0.4693 0.4148 0.3666 0.3241 0.2865... 0.2532 0.2238 0.1546]; plot(x,y,x,y,'*'); %分别对x,y进行对数变换 x1=log(x); y1=log(y); figure; plot(x1,y1);

运行结果：

由此可推断出x与y之间类似对数关系，如下：

$lny=alnx+b$

可以利用线性函数拟合的方法来得出线性参数 $a,b,e^b$ ，如下：

$y=e^bx^a$

第二步：拟合求解参数

MATLAB代码如下：

clc;clear; %数据分析 x=[1.1052 1.2214 1.3499 1.4918 1.6487 1.8221 2.0138 2.2255... 2.4596 2.7183 3.6693]; y=[0.6795 0.6006 0.5309 0.4693 0.4148 0.3666 0.3241 0.2865... 0.2532 0.2238 0.1546]; %分别对x,y进行对数变换 x1=log(x); y1=log(y); %求解参数 A=[x1',ones(size(x1'))]; c=[A\y1']'; a=c(1) b=exp(c(2))

运行结果：

a =-1.233846992794170 b =

0.768715215732740

所以最终的拟合函数为：

$y(x)=0.768715215732740e^{-1.233846992794170}$

例题5

对函数f(x)进行多项式拟合，可以选择各个函数为 $f_i(x)=x^{n+1-i},\quad i=1,2,\cdots,8$ 。

$f(x)=(x^2-3x+5)e^{-5x}sinx$

解：

MATLAB代码如下：

clc;clear; n=8; x=[0:0.1:1]'; y=(x.^2-3*x+5).*exp(-5*x).*sin(x); A=[]; for i=1:n+1, A(:,i)=x.^(n+1-i); end c=A\y; vpa(poly2sym(c),5) %表示为多项式形式

运行结果：

ans = - 8.2586*x^8 + 43.566*x^7 - 101.98*x^6 + 140.22*x^5 - 125.29*x^4 + 74.45*x^3 - 27.672*x^2 + 4.9869*x + 4.2037e-7

【本文地址】

基于MATLAB解决数据拟合的振荡现象（附完整代码与算法）

基于MATLAB解决数据拟合的振荡现象（附完整代码与算法）

今日新闻

推荐新闻