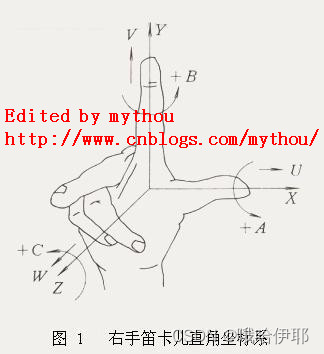
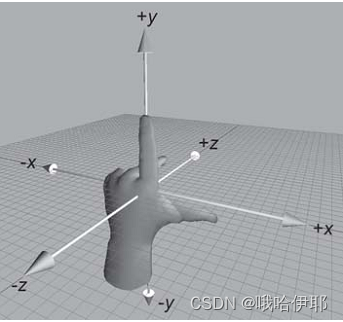
最近在做规划控制的坐标系转换时，发现之前遗留的坐标系问题没有解决，因此单独整理一下。

对于单位坐标系，一般分为左手坐标系和右手坐标系，他们的区别在于三个坐标轴的组合。

在三维坐标系中，Z轴的正轴方向是根据右手定则确定的，右手定则也决定三维空间中任一坐标轴的正旋转方向。要标注X、Y和Z轴的正轴方向，就将右手背对着屏幕放置，拇指即指向X轴的正方向，伸出食指和中指，如下图所示，食指指向Y轴的正方向，中指所指示的方向即是Z轴的正方向。

伸出左手，让拇指和食指成“L”型，大拇指向右，食指向上。其余的手指指向前方，这样就建立了一个左手坐标系。拇指、食指和其余手指分别代表X、Y和Z轴的正方向。

也叫地心地固坐标系（Earth-Centered,Earth-Fixed，简称ECEF）简称地心坐标系，是一种以地心为原点的地固坐标系（也称地球坐标系），是一种笛卡儿坐标系。原点 O (0,0,0)为地球质心，Z 轴与地轴平行指向北极点，X轴指向本初子午线与赤道的交点，Y轴垂直于XOZ平面(即东经90度与赤道的交点)构成右手坐标系。

也叫经纬高坐标系（LLA坐标系）、全球地理坐标系、大地坐标系。可以说是最为广泛应用的一个地球坐标系，能够给出一点的大地纬度、大地经度和大地高程而更加直观地告诉我们该点在地球中地位置。 一句话就是把前面提到地ECEF坐标系用在GPS中，就是WGS-84坐标系。

也叫站心坐标系、站点坐标系、东-北-天坐标系，英文名称是local Cartesian coordinates coordinate system，以用户所在位置P为坐标原点。坐标定义为：X轴指向东，Y轴指向北，Z轴指向天顶。 ENU局部坐标系采用三维直角坐标系来描述地球表面，实际应用较为困难，因此一般使用简化后的二维投影坐标系来描述。在众多二维投影坐标系中，统一横轴墨卡托（The Universal Transverse Mercator ，UTM）坐标系是一种应用较为广泛的一种。UTM坐标系统使用基于网格的方法表示坐标，他将地球分为60个经纬区，每个区包含6度的经度范围，每个区内的坐标均基于横轴墨卡托投影。

LLA坐标系下的(lon,lat,alt)转换为ECEF坐标系下点(X,Y,Z)： { X = ( N + a l t ) c o n t ( l a t ) c o s ( l o n ) Y = ( N + a l t ) c o s ( l a t ) s i n ( l o n ) Z = ( N ( 1 − f ) 2 + a l t ) s i n ( l a t ) ) \left\{ \begin{matrix} X=(N + alt)cont(lat)cos(lon) \\ Y= (N + alt)cos(lat)sin(lon) \\ Z = (N(1 - f)^2 + alt)sin(lat)) \end{matrix} \right. ⎩ ⎨ ⎧​X=(N+alt)cont(lat)cos(lon)Y=(N+alt)cos(lat)sin(lon)Z=(N(1−f)2+alt)sin(lat))​

其中，f为极扁率，N为基准椭球体的曲率半径 N = a 1 − f ( 2 − f ) ∗ s i n 2 ( l a t ) N= \frac{a}{\sqrt{1 - f(2-f)*sin^2(lat)}} N=1−f(2−f)∗sin2(lat) ​a​

ECEF坐标系下点(X,Y,Z)转换为LLA坐标系下的(lon,lat,alt) l o n = a r c t a n ( y x ) a l t = p c o s ( l a t ) − N l a t = a r c t a n [ z p ( 1 − e 2 N N + a l t ) − 1 ] p = x 2 + y 2 lon = arctan(\frac{y}{x}) \\ alt = \frac{p}{cos(lat) - N} \\ lat = arctan[\frac{z}{p}\left(1 - e^2\frac{N}{N + alt}\right)^{-1}] \\ p = \sqrt{x^2 + y^2} lon=arctan(xy​)alt=cos(lat)−Np​lat=arctan[pz​(1−e2N+altN​)−1]p=x2+y2 ​ 一开始lon是未知的，可以假设为0，经过计策迭代之后就能收敛。

用户所在坐标原点 P 0 = ( x 0 , y 0 , z 0 ) P_0 =(x_0,y_0,z_0) P0​=(x0​,y0​,z0​)，计算点 P = ( x , y , z ) P=(x,y,z) P=(x,y,z)，在以点 P 0 P_0 P0​为坐标原点的ENU坐标系位置(e,n,u)，这里需要用到LLA坐标系的数据， P 0 P_0 P0​的LLA坐标点为 L L A 0 = ( l o n 0 , l a t 0 , a l t 0 ) LLA_0=(lon_0,lat_0,alt_0) LLA0​=(lon0​,lat0​,alt0​)

[ Δ x Δ y Δ z ] = [ x y z ] − [ x 0 y 0 z 0 ] \begin{bmatrix} \Delta x \\ \Delta y \\ \Delta z \end{bmatrix} = \begin{bmatrix} x \\ y \\ z \end{bmatrix} -\begin{bmatrix} x_0 \\ y_0 \\ z_0 \end{bmatrix} ​ΔxΔyΔz​ ​= ​xyz​ ​− ​x0​y0​z0​​ ​ [ e n u ] = S ⋅ [ Δ x Δ y Δ z ] = S ⋅ [ − s i n ( l o n 0 ) c o s ( l o n 0 ) 0 − s i n ( l a t 0 ) c o s ( l o n 0 ) − s i n ( l a t 0 ) s i n ( l o n 0 ) c o s ( l a t 0 ) c o s ( l a t 0 ) c o s ( l o n 0 ) c o s ( l a t 0 ) s i n ( l o n 0 ) s i n ( l a t 0 ) ] = S ⋅ [ Δ x Δ y Δ z ] \begin{bmatrix} e \\ n\\ u \end{bmatrix} =S \cdot \begin{bmatrix} \Delta x \\ \Delta y \\ \Delta z \end{bmatrix} =S \cdot \begin{bmatrix} -sin(lon_0)&cos(lon_0)&0 \\ -sin(lat_0)cos(lon_0)&-sin(lat_0)sin(lon_0)&cos(lat_0) \\ cos(lat_0)cos(lon_0)&cos(lat_0)sin(lon_0)&sin(lat_0) \end{bmatrix} =S \cdot \begin{bmatrix} \Delta x \\ \Delta y \\ \Delta z \end{bmatrix} ​enu​ ​=S⋅ ​ΔxΔyΔz​ ​=S⋅ ​−sin(lon0​)−sin(lat0​)cos(lon0​)cos(lat0​)cos(lon0​)​cos(lon0​)−sin(lat0​)sin(lon0​)cos(lat0​)sin(lon0​)​0cos(lat0​)sin(lat0​)​ ​=S⋅ ​ΔxΔyΔz​ ​

S为单位正交矩阵 S − 1 = S T S^{-1} = S^T S−1=ST 反之 [ Δ x Δ y Δ z ] = S − 1 ⋅ [ e n u ] = S T ⋅ [ e n u ] \begin{bmatrix} \Delta x \\ \Delta y \\ \Delta z \end{bmatrix} =S^{-1} \cdot \begin{bmatrix} e \\ n\\ u \end{bmatrix} = S^T \cdot \begin{bmatrix} e \\ n\\ u \end{bmatrix} ​ΔxΔyΔz​ ​=S−1⋅ ​enu​ ​=ST⋅ ​enu​ ​

上述可以看到，从LLA坐标系转换到enu坐标系有较多计算量，在考虑地球偏心率ee很小的前提下，可以做一定的近似公式计算 [ Δ e Δ n Δ u ] = [ a ⋅ c o s ( l a t ) ⋅ Δ l o n 0 0 0 a ⋅ l a t 0 0 0 Δ a l t ] \begin{bmatrix} \Delta_e \\ \Delta_n\\ \Delta_u \end{bmatrix} =\begin{bmatrix} a\cdot cos(lat)\cdot \Delta lon&0&0 \\ 0&a\cdot lat&0 \\ 0&0&\Delta alt \end{bmatrix} ​Δe​Δn​Δu​​ ​= ​a⋅cos(lat)⋅Δlon00​0a⋅lat0​00Δalt​ ​

转载自 https://zhuanlan.zhihu.com/p/404773542

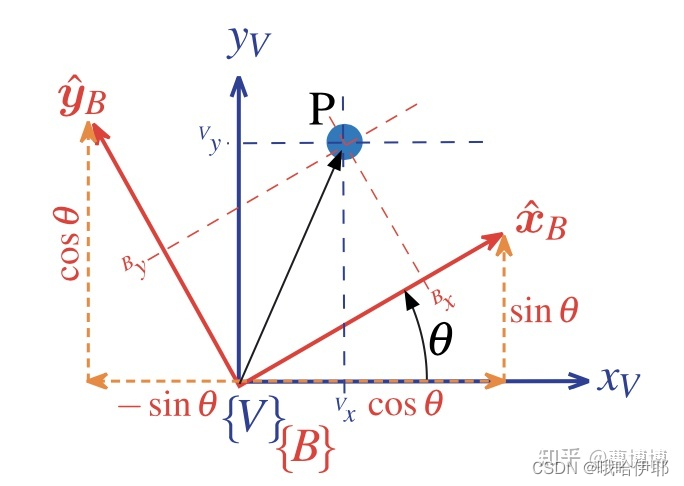这张图可以很好地解释旋转矩阵的用法，这里有两个坐标系V和B，P点在这个空间中是一个固定的点，在不同坐标系下的表达是不一样的，比如在B坐标系里面，坐标是