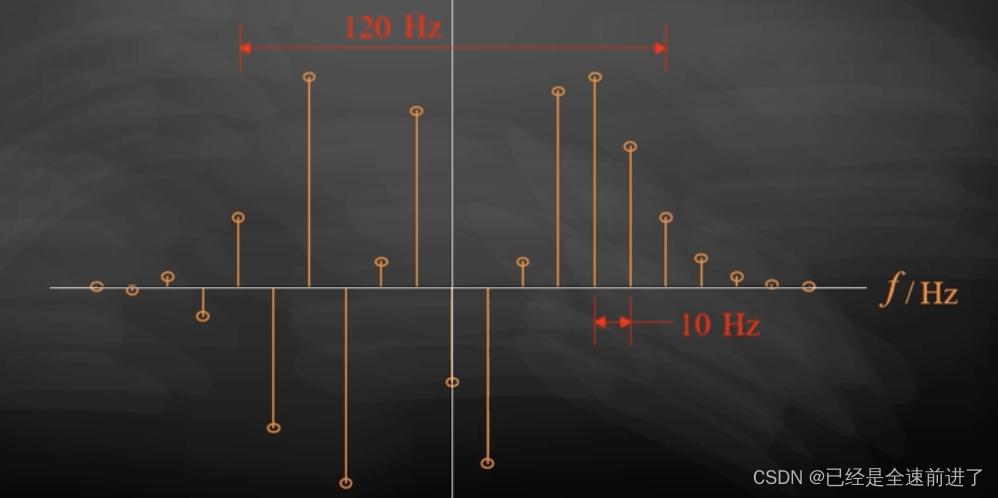
在之前介绍的几种调制方式中，我提到信噪比时计算的是用户解调后的信噪比，然而在北邮通信原理课中考虑的是解调器输入的信噪比，即考虑的信号功率是经过BPF之后进行解调之前的部分。

之前没有注意到这个差异，非常抱歉。笔者在本科学习通信原理的时候也是认为与其记解调输入信噪比的结果，不如弄清楚每一处的信号组成，这样不管求什么信噪比都能求。

下面我们开始学习角度调制的内容，包括调频FM与调相PM。

注：在本章中，偶尔会忘记了写幅度系数 A c A_c Ac​，只是一个常数不影响结论，所以我有时候嫌麻烦就不写了。在具体问题中如果调制信号或载波信号中有幅度系数可不要忘记了。

首先需要弄清楚什么是相位、频率。考虑一个复包络信号：

s L ( t ) = A ( t ) e j ϕ ( t ) s_L(t)=A(t)e^{j\phi(t)} sL​(t)=A(t)ejϕ(t) 用欧拉公式展开得 = A ( t ) [ cos ⁡ ϕ ( t ) + j sin ⁡ ϕ ( t ) ] =A(t)\left[\cos\phi(t)+j\sin\phi(t)\right] =A(t)[cosϕ(t)+jsinϕ(t)]

其中 A ( t ) A(t) A(t)称为幅度， ϕ ( t ) \phi(t) ϕ(t)为相位，它表示的是一种角度与时间的函数关系。相位变化的快慢定义为瞬时角频率，在北邮通信原理中习惯用瞬时频率 f ( t ) = 1 2 π d ϕ ( t ) / d t f(t)=\frac{1}{2\pi}d\phi(t)/dt f(t)=2π1​dϕ(t)/dt。（角频率即 ω ( t ) = 2 π f ( t ) \omega(t)=2\pi f(t) ω(t)=2πf(t)，正弦信号的频率是定值）

调频和调相是让调制信号作为已调信号的复包络的频率和相位的一部分来实现调制传输。根据这个思路我们先给出调相信号PM：

s P M ( t ) = cos ⁡ ( 2 π f c t + K p m ( t ) ) s_{PM}(t)=\cos(2\pi f_ct+K_pm(t)) sPM​(t)=cos(2πfc​t+Kp​m(t))

f c f_c fc​为载波频率，在正弦信号中一般称 2 π f c t 2\pi f_ct 2πfc​t以为的部分为相位偏移。调相就是将调制信号作为复包络的瞬时相偏， K p K_p Kp​为常数。对瞬时相偏求导在除掉 2 π 2\pi 2π就能得到瞬时频偏，将调制信号作为复包络的瞬时频偏即可得到调频信号FM：

s F M ( t ) = cos ⁡ ( 2 π f c t + 2 π K f ∫ − ∞ t m ( τ ) d τ ) s_{FM}(t)=\cos(2\pi f_ct +2\pi K_f\int_{-\infty}^tm(\tau)d\tau) sFM​(t)=cos(2πfc​t+2πKf​∫−∞t​m(τ)dτ)

验证一下，对上式中的瞬时相偏 2 π K f ∫ − ∞ t m ( τ ) d τ 2\pi K_f\int_{-\infty}^tm(\tau)d\tau 2πKf​∫−∞t​m(τ)dτ求导除去 2 π 2\pi 2π得到 K f m ( t ) K_fm(t) Kf​m(t)， K f K_f Kf​为常数。这里所提的调频调相都是线性的，即瞬时相偏与瞬时频偏都与调制信号的关系是线性的。

此外，容易看出来调相与调频的关系就是一个微分的关系，先对调制信号求微分在进行调相就等价于调频。因此，调频与调相可以轻松地进行等价，后面的分析便以调频为例进行，不必再单独对调相进行重复的分析。

在介绍幅度调制时，已调信号的频谱没有单独去细讲，利用复包络的性质很容易能得到其频谱就是原信号频谱（或单边带、或叠加载波）的左右搬移。然而角度调制的频谱却无法这样得到，因为复包络的频谱不再是那么容易由原信号的频谱获得，考虑FM信号的复包络：

s L ( t ) = e j 2 π K f ∫ − ∞ t m ( τ ) d τ s_L(t)=e^{j2\pi K_f\int_{-\infty}^tm(\tau)d\tau} sL​(t)=ej2πKf​∫−∞t​m(τ)dτ

注意，这可不是复单频信号，它的频率不是固定的常数，而是一个变化的函数，取决于调制信号的表达式，因此其傅里叶变换并不好求。

让我们将问题退化到一个简单的情形，考虑当 m ( t ) = cos ⁡ 2 π f m t m(t)=\cos2\pi f_mt m(t)=cos2πfm​t为一个单频信号时（正弦信号），求其FM信号的频谱。先给出FM信号的表达式如下：

s F M ( t ) = cos ⁡ ( 2 π f c t + 2 π K f ∫ − ∞ t cos ⁡ 2 π f m τ d τ ) s_{FM}(t)=\cos(2\pi f_ct+2\pi K_f\int_{-\infty}^t\cos2\pi f_m\tau d\tau) sFM​(t)=cos(2πfc​t+2πKf​∫−∞t​cos2πfm​τdτ) = cos ⁡ ( 2 π f c t + K f f m sin ⁡ 2 π f m t ) =\cos(2\pi f_ct+\frac{K_f}{f_m}\sin2\pi f_mt) =cos(2πfc​t+fm​Kf​​sin2πfm​t)

已知调频是用调制信号表示复包络的瞬时频偏，那么瞬时频偏的最大值 Δ f max ⁡ \Delta f_{\max} Δfmax​容易得到就是 K f K_f Kf​。再定义调频指数 β = Δ f max ⁡ / f m = K f / f m \beta=\Delta f_{\max}/f_m=K_f/f_m β=Δfmax​/fm​=Kf​/fm​。从而复包络可以表示为：

s L ( t ) = e j β sin ⁡ 2 π f m t s_L(t)=e^{j\beta\sin2\pi f_mt} sL​(t)=ejβsin2πfm​t

这是一个周期信号，可以进行傅里叶级数展开，然后再对展开的复单频率信号进行傅里叶变换，从而得到频域表达式：

s L ( t ) = ∑ n = − ∞ ∞ J n ( β ) e j 2 π n f m t s_L(t)=\sum_{n=-\infty}^{\infty}J_n(\beta)e^{j2\pi nf_mt} sL​(t)=∑n=−∞∞​Jn​(β)ej2πnfm​t S L ( f ) = ∑ n = − ∞ ∞ J n ( β ) δ ( f − n f m ) S_L(f)=\sum_{n=-\infty}^{\infty}J_n(\beta)\delta(f-nf_m) SL​(f)=∑n=−∞∞​Jn​(β)δ(f−nfm​)

其中 J n ( β ) J_n(\beta) Jn​(β)是该傅里叶级数展开式的系数，它是一个特殊的函数——称为第一类 n n n阶贝塞尔函数。可见该复包络的频谱由无数个冲激组成，然而当 n n n增大时， ∣ J n ( β ) ∣ |J_n(\beta)| ∣Jn​(β)∣会趋近于0，因此该复包络的频谱主要集中在基带。 J n ( β ) J_n(\beta) Jn​(β)还具有如下性质:

当 n 为偶数时： J n ( β ) = J − n ( β ) 当n为偶数时：J_n(\beta)=J_{-n}(\beta) 当n为偶数时：Jn​(β)=J−n​(β) 当 n 为奇数时： J n ( β ) = − J − n ( β ) 当n为奇数时：J_n(\beta)=-J_{-n}(\beta) 当n为奇数时：Jn​(β)=−J−n​(β)

下图是一个单频信号的频谱例图，可以看出其幅值满足上述的关系式。

上述结果当 m ( t ) m(t) m(t)为单频信号时，调频信号的频谱特性，然而一般信号难以进行频谱分析，不过可以通过卡松公式进行带宽分析，该公式给出了FM信号的带宽的估计值：

B ≈ 2 Δ f m a x + 2 f m = 2 β f m + 2 f m B\approx 2\Delta f_{max}+2f_m=2\beta f_m+2f_m B≈2Δfmax​+2fm​=2βfm​+2fm​

其中 f m f_m fm​为基带信号的最高频率，因此，只需知道最大频偏与基带信号的最高频率，即可进行FM信号的带宽估计。

如果是PM信号，可以将原信号 m ( t ) m(t) m(t)求积分得到新的信号 x ( t ) = ∫ − ∞ t m ( τ ) d τ x(t)=\int_{-\infty}^tm(\tau)d\tau x(t)=∫−∞t​m(τ)dτ，则PM信号便可以看作 x ( t ) x(t) x(t)的FM信号，再应用卡松公式进行求解。

然而上述过程其实可以简化，通过傅里叶变换的积分特性，我们可得 X ( f ) = M ( f ) / j 2 π f X(f)=M(f)/j2\pi f X(f)=M(f)/j2πf，从而可知 x ( t ) x(t) x(t)与 m ( t ) m(t) m(t)的最高频率相同，而最大频偏是由已调信号的形式所确定的。因此，我们不需要求出原信号 x ( t ) x(t) x(t)，直接用原信号的最大频率与最大频偏即可求出带宽估计值。

综合上述的结果，我们还可以进一步精简我们的结论，即只要我们有角度调制信号 s ( t ) = cos ⁡ ( 2 π f c t + x ( t ) ) s(t)=\cos(2\pi f_ct + x(t)) s(t)=cos(2πfc​t+x(t))，我们不需要去管它到底是FM调制还是PM调制，也不需要管它的原信号是什么，只需要利用 x ( t ) x(t) x(t)求出最大频偏与最大频率，即可完成带宽估计。（其实这个结论是合理的，因为已调信号的表达式才是决定带宽的，而这个表达式本身并不能体现其使用的调制方法。）

至于卡松公式本身的记忆其实也并不困难，原信号的最大频率可以理解为原基带信号的带宽估计，再其基础上往右偏移最大的结果就是叠加上最大频偏，因此带宽估计变为 Δ f max ⁡ + f m \Delta f_{\max}+f_m Δfmax​+fm​，然后再搬移到频带，带宽变为两倍。

本文对角度调制信号的表达式与频谱特性进行了介绍，其中频谱特性这一块省略了具体的推导（即为什么傅里叶级数的系数是贝塞尔函数）。可以当作结论使用即可，其实更加重要的是卡松公式的理解，它给出了角度调制信号的带宽估计值，这对实际通信系统来说更加有意义，毕竟在调制的时候我们更关心的可能是已调信号的带宽而不是具体的频谱形状。

下一篇将会单独对角度调制信号的抗噪声性能进行学习。