作为一个工程师，很多人对随机振动看着熟悉，却又实际陌生。熟悉是因为几乎每个产品在出厂时都要求要做随机振动试验，陌生是因为当面对用户所给的功率密度谱有时会感到很茫然，尤其是这个功率谱的单位居然是 g^2/Hz ，简直是反人类，为啥整这么麻烦，不能给个加速度 g 直接振吗？哈哈，这个还真不能，下面咱们就来抽丝剥茧，看看随机振动功率密度谱到底是咋个回事？

随机振动，是因为振动源是随机信号，顾明思议，就是信号的发生带有随机性，无法用一个明确的函数把它表达出来，一个典型的随机信号大概长这个样子：

可以看出，乍一看完全没有规律可言，高度不规则，无规律的，不可预估也不可重复，每次测量都不一样。那随机信号是不是就是不可描述的呢？首先我们研究一下什么是随机，随机对应不确定性，不确定性在物理学和数学上是一个不受欢迎的词，老板问你图纸什么时候画完，你敢回答“随机吧”，或者更佛系一点“随缘吧”？相信等待你的可不仅仅是白眼哦，这也是为啥当初波恩将概率解释引入到量子力学时受到爱因斯坦强烈的反对，“上帝是不掷骰子”的典故便来源于此。然后诸多证据表明：也许随机是这个世界的本质特性之一，这可以由一个著名的数学定理来证明：中心极限定理。

一、随机信号和正态分布有什么关系

中心极限定理有一组，但基本可以用一句通俗的话来概括它们：大量相互独立的随机变量，其平均值正态分布。对中心极限定理最形象的解释是高尔顿钉板实验：小球在下落过程中碰到很多个钉子，每次碰撞都是一个二项式的随机过程：以同等的概率通过钉子左侧或者右侧，小球最后到达的位置，是这很多个“左右”随机变量相加后的平均位置。不难看出，这个平均值落在中心处的概率最大，小球聚集最多，但也可能向左或向右偏，偏离越大，小球的数目越少，不同位置的不同小球数便形成了一个“分布”，中心极限定理则是从数学上证明了，这个分布的极限是正态分布。

高尔顿钉板实验实质上是一组二项式分布，从数学上还可以证明：中心极限定理的条件可以从二项分布推广到独立同分布随机序列，以及不同分布的随机序列。也就是说：在一定条件下，各种随意形状概率分布生成的随机变量，它们加在一起的总效应，是符合正态分布的。这也是为啥正态分布这么常见的原因，因为实际上的随机生物过程或物理过程，都不是只由一个单独的原因产生的，它们受到各种各样随机因素的影响。比如产品加工免不了有误差，而误差形成的原因五花八门，各种各样。就算我们打开上帝视角，够分别清楚产生误差的每种单一原因，误差的分布曲线可能不是高斯的，但是，所有误差加累计在一起时，通常得到一个正态分布。下图是30组随机变量，和值随数据增加时分布情况。

总之，中心极限定理告诉我们：无论引起过程的各种因素的基本分布是什么样的，当实验次数 充分大时，所有这些随机分量之和近似是一个正态分布的随机变量。也就是说：对于平稳随机过程而言，其分布是趋于正太的。

我们知道，正态分布的概率密度的表达式为：

p(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{\frac{(x-\mu)^2}{2\sigma^2}}

其中 \mu 为数学期望，代表着信号的平均值，

\mu=\lim_{T \rightarrow \infty}{\frac{1}{T}}\int_{0}^{T}x(t)dt，

\sigma^2 为方差，表示这信号偏离平均值的程度，

\sigma^2=\lim_{T \rightarrow \infty}{\frac{1}{T}}\int_{0}^{T}(x(t)-\mu)^2dt 。

\Psi^2 为均方值，在工程上可以一般看成信号的平均功率，其平方根为有效值（RMS值），

\Psi^2=\lim_{T \rightarrow \infty}{\frac{1}{T}}\int_{0}^{T}[x(t)]^2dt

很容易得到：

\Psi^2=\sigma^2+\mu^2

所以当平均值为零的时候，均方值与方差相等。从图形上看，平均值\mu 决定了正态分布的位置，均方根值，也就是标准差 \sigma ，决定了分布的幅度。如果正态分布概率密度一旦确定，其数学期望 \mu 和方差 \sigma^2 也就确定了。对于随机信号而言，数学期望 \mu 基本为零（或者去除直流分量后为零），所以唯一确定的量就剩均方值，此时均方值和方差一致，并且

\Psi^2=\lim_{T \rightarrow \infty}{\frac{1}{T}}\int_{0}^{T}\left| x(t) \right|^2dt

如果仔细观察上式，可以发现，从量纲来看， \int_{0}^{T}\left| x(t) \right|^2dt 代表了能量概念，而方差 {\frac{1}{T}}\int_{0}^{T}\left| x(t) \right|^2dt 代表了平均功率概念。

前面我们说到，平稳随机信号是趋于正态分布的，决定正态分布的两个参数：平均值 \mu 基本为零（不为零时，直流分量也很容易处理），唯一能表征随机信号的就剩均方值（ \mu=0 时等于方差）\Psi^2 ，也就是平均功率了。再具体一点，对于平稳随机信号而言，描述 x(t) 是没有意义的，描述平均功率才有意义。如何才能描述平均功率呢？这时我们就要用到频谱分析的概念了，可能有些人会觉得这个概念很生疏，我要说我们每天一睁眼就在进行谱分析你会信吗？事实还真是这样。我们的眼睛就是一双最精密的谱分析仪：过滤到可见光以外的所有光线，并且可见光按照频谱（频率）进行精确分类。我们知道光本质是一种电磁波，既然是波，就有波长 \lambda 和波动频率 f ，光速 c=\lambda\cdot f 一个定值，波长和波动频率成反比。人眼可识别出波长在400纳米至700纳米的光线，并且根据波长不同（频率不同）将可见光分成红、橙、黄、绿、蓝、靛、紫色。当我们说“一个东西的表面是红色”的时候，这是正常人的定性描述，换成喜欢定量描述（装X）工程师会怎么说呢？“这个东西表面特性会选择性反射一种电磁波，这种电磁波波长约700纳米，波动频率 约5\times10^{14} 赫兹”。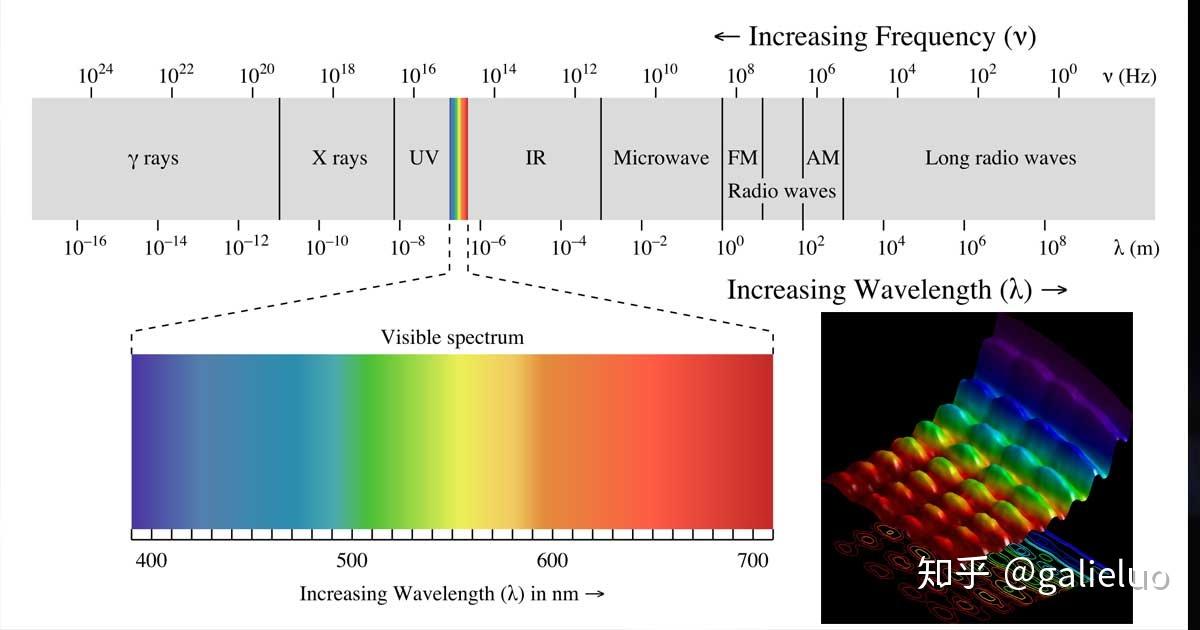

那频谱分析是什么呢？它是一种将复杂号分解为较简单信号的技术，许多物理信号均可以表示为许多不同频率简单信号的和，找出一个信号在不同频率下的信息（可能是幅度、功率、强度或相位等）的作法就是频谱分析。比如通过一个三棱镜就可进行色散试验，将白光分解成频率各不相同的单色光，我们经常在雨后见到的彩虹也是一种色散现象。

图片来源：http://www.bolvan.ph.utexas.edu

在傅里叶变换背后到底有什么小秘密 这篇文章中，我们介绍了傅里叶变换概念，它是频谱分析的基础，这篇文章中介绍了复指数函数是如何构成一个完备正交基的，以及如何进行傅里叶变换及其逆变换。但是，说这么多，频谱分析和随机信号有什么关系？

二、时域、频域之间功率守恒？

频谱分析和平稳随机信号可以通过一个叫“帕斯瓦定理”的公式联系起来，一个经常被低估的定理，大概长这个样子：

\int_{-\infty}^{+\infty}\left| x(t) \right|^2dt=\frac{1}{2\pi}\int_{-\infty}^{+\infty}\left| F_x(\omega) \right|^2d\omega=\int_{-\infty}^{+\infty}\left| F_x(2\pi f) \right|^2df

其中 F(\omega) 是 x(t) 的傅里叶变换，这个公式看着还挺对称，被积函数都是自变量的平方，貌似蕴含着什么深刻的意义。翻译过来，这个定理说的是什么事呢？那就是信号的能量（或者平均功率）无论在时域看，还是在频域看，都是一样的。人类习惯于在时域观察一个信号，那会不会存在另一个物种或者空间，他们喜欢在频域观察呢？但无论如何，帕斯瓦定理告诉我们，不论频域还是时域，信号所代表的能量是守恒的，而守恒的本质是对称性，那是不是预示着时域和频域有着某种高度的对称呢？

好了，扯远了，哲学上的事情不归工程师管，我们要所的事情就是如何定量化的的去描述不确定的东西，比如随机信号。前面我们说了，平稳随机信号 x(t) 的幅值是呈现正太分布的，其平均值接近为零（或去除直流分量后），均方值或方差（也就是平均功率）是固定的，既然平均功率（或能量）在时域和频域是守恒的，而在时域 x(t) 是随机的，不可描述，那我们可以换到频域去啊：

\lim_{T \rightarrow \infty}{\frac{1}{T}}\int_{0}^{T}\left| x(t) \right|^2dt=\lim_{T \rightarrow \infty}{\frac{1}{T}}\int_{-\infty}^{+\infty}\left| F_x(2\pi f) \right|^2df=\int_{-\infty}^{+\infty} S_x(f) df

其中： S_x(f)=\lim_{T \rightarrow \infty}\frac{1}{T}{\left| F_x(2\pi f) \right|^2} ， S_x(f) 表示了信号的平均功率（或能量）在频域上的分布，即单位频带的功率随频率变化的情况，故称之为信号的自功率谱密度函数，简称自功率谱或自谱。 S_x(f) 与 f 轴包围的面积等于信号 x(t) 的平均功率，即 x(t) 的幅值分布的方差或均方值。同时可以看出，当 x(t) 表示加速度时（单位为 g ）， S_x(f) 的单位就变成了 g^2/Hz。

三、自相关又是个什么玩意？

现在，事情就貌似变得简单了，我们将时域信号 x(t) 进行傅里叶变换，得到频域分布 F(\omega) ,然后平方积分就可以得到功率谱密度了啊。理论上，我们确实可以这么做，但是实际上，这样做有一个小困难，那就是经典傅里叶变换不是一直存在的，前提的：信号 x(t) 绝对值可积，即 \int_{-\infty}^{+\infty}\left| x(t) \right|dt\prec +\infty ，而实际上平稳随机变量是不满足的。为了解决随机信号的傅里叶变换问题，我还得引入一个概念：自相关，先看定义：随机过程 x(t) 的自相关函数定义为在时刻 t 和时刻 t+\tau 的随机变量乘积的平均值， \tau 是时移，当平均时间 T\rightarrow\infty 时，平均值的极限便是自相关函数，其数学表达式为：

R_x(\tau)=\lim_{T\rightarrow \infty}\frac{1}{T}\int_{-\infty}^{+\infty}x(t)x(t+\tau)dt 定义有点拗口，可以先不理解，它说明一个什么事呢？它反映了随机信号本身在不同时刻的相互关系，再直白一点：把一个信号平移一段距离，跟原来有多相似。我们都知道，重要的证件上的照片，一般都要求是近半年的，道理显而易见，时间久了跟现在长得可能就不一样了。下图显示了C罗近十年容颜的变化，都说女大十八变（即使不整容），男的又何尝不是。

很显然的一点是：随着时间的推移，C罗的长相是发生明显变化的，时间越短，长相越接近，可以想象，当时间足够长后，不知道我们还能不能认出他来，不信，你看：

对于随机信号，特别白噪声随机信号来说，当时移 \tau 非常小时， x(t) 和 x(t+\tau) 相差很小的概率很大，这时 R_x(\tau\rightarrow0) 值非常大，表示关系密切。特别当 \tau=0 时， R_x(\tau=0) 值最大，等于方均值，也就是平均功率，表示完全相关。当时移 \tau 较大时， x(t) 和 x(t+\tau) 相差很小的概率很小。作平均计算正负对消， R_x(\tau) 值很小。并且随着 \tau 值的增大， R_x(\tau\rightarrow\infty) 值很快衰减到零，表示 x(t) 和 x(t+\tau) 之间没有依赖关系，对一般的宽带随机振动，时间间隔很远的二个随机量之间不存在任何固定关系。简单点来说：对于平稳随机信号，自相关函数将信号的平均功率向 \tau=0 这一点集中， \tau\ne0 时自相关函数快速衰减为零。

R_x(0)=\lim_{T\rightarrow \infty}\frac{1}{T}\int_{-\infty}^{+\infty} x(t)\cdot x(t)dt

对于周期信号，自相关函数可以把随机信号中的周期成份检测出来，这是因为任何周期信号在所有的时移上都有一定形状的自相关函数图形。对于周期信号来说，经过一个周期后又精确的重复过去的时间历程，因此当时移超过该周期时，其自相关函数必然重复前一段的形状。所以若在自相关函数图上发现时移趋于无穷大， R_x(\tau\rightarrow\infty)\ne0 ，而有某种周期性，则说明该随机振动信号混有周期信号成分。 简单点来说：自相关函数能够检测出信号内部蕴藏的周期组分，而过滤掉了周期组分的相位信息。

对于上面两段话不是很理解的，可以看下面两幅图，分别是白噪声随机信号和随机相位正弦信号及其自相关信号。

说了这么多，和我们要进行功率谱分析有什么关系？前面我们分析了，信号的功率在时域和频域都是满足守恒定律的，

\lim_{T \rightarrow \infty}{\frac{1}{T}}\int_{0}^{T}\left| x(t) \right|^2dt=\lim_{T \rightarrow \infty}{\frac{1}{T}}\int_{-\infty}^{+\infty}\left| F_x(2\pi f) \right|^2df

而功率被定义成幅值的平方的时间平均分量，而这个过程，也可以看成是去除频域谐波分量的相位信息的过程，因为本质来说，一个简谐信号的相位是不影响其功率的。而自相关函数，也具有去除信号相位的功能，那自相关函数和功率密度谱是不是有什么深刻的联系呢？答案是肯定的，那就是维纳-辛钦定理（Wiener–Khinchin theorem），这个定理表明：信号的自相关函数与功率密度谱是一对傅里叶变换对：

S_x(f)=\int_{-\infty}^{+\infty}R_x(\tau)e^{-i2\pi f\tau}d\tau

R_x(\tau)=\int_{a}^{b}S_x(f)e^{i2\pi f\tau}df

也就是说：一个信号的功率密度谱，就是其自相关函数的傅里叶变换。

总结一下整个逻辑：对于一个随机信号而言，时域信息是杂乱无章的，唯一的确定性信息但是在统计意义下得到的，即幅值呈正太分布，均方值也就是平均功率是固定的。根据帕斯瓦定理，信号的平均功率在时域和频域是守恒的，按道理说直接对时域信号进行傅里叶变换再取平方就可以。但不幸的事，随机信号的不满足傅里叶变换绝对值可积的条件，严格意义傅里叶变换不存在，于是发明了自相关函数的概念，将信号的蕴含的周期信号识别出来，并将相位信息去掉（相位不影响平均功率），于是就出现了我们在教材上见到的最终形式维纳-辛钦定理：一个信号的功率密度谱，就是其自相关函数的傅里叶变换。提炼一下就是：随机信号→幅值正太分布→均方值（平均功率）→帕斯瓦定理（功率守恒）→自相关函数（去除相位信息）→维纳-辛钦定理（最终形式）。