二次曲面 |
您所在的位置：网站首页 › 17种二次曲面方程按中心分类 › 二次曲面 |
二次曲面
|
在解析几何中，二次曲面是指空间中曲面方程是二次式的曲面，它一共有17种（包括退化情形）。 目录 1 一般方程 2 方程的化简 2.1 转轴 2.2 移轴 3 二次曲面的主方向 4 二次曲面种类 一般方程二次曲面的一般方程是 F ( x , y , z ) = a 11 x 2 + a 22 y 2 + a 33 z 2 + 2 a 12 x y + 2 a 13 x z + 2 a 23 y z + 2 a 1 x + 2 a 2 y + 2 a 3 z + a 0 = 0 {\displaystyle F(x,y,z)=a_{11}x^{2}+a_{22}y^{2}+a_{33}z^{2}+2a_{12}xy+2a_{13}xz+2a_{23}yz+2a_{1}x+2a_{2}y+2a_{3}z+a_{0}=0} 其中 a 11 , a 22 , a 33 , a 12 , a 13 , a 23 {\displaystyle a_{11},a_{22},a_{33},a_{12},a_{13},a_{23}} 不全为零。方程的二次项部分记作 φ ( x , y , z ) = a 11 x 2 + a 22 y 2 + a 33 z 2 + 2 a 12 x y + 2 a 13 x z + 2 a 23 y z {\displaystyle \varphi (x,y,z)=a_{11}x^{2}+a_{22}y^{2}+a_{33}z^{2}+2a_{12}xy+2a_{13}xz+2a_{23}yz} ，这是一个三元二次型，它所对应的矩阵常记为 A 1 = ( a i j ) 3 × 3 = ( a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ) {\displaystyle A_{1}=(a_{ij})_{3\times 3}={\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{pmatrix}}} 。原二次曲面方程可以形式的写作如下矩阵方程 ( x , y , z , 1 ) ( a 11 a 12 a 13 a 1 a 21 a 22 a 23 a 2 a 31 a 32 a 33 a 3 a 1 a 2 a 3 a 0 ) ( x y z 1 ) = 0 {\displaystyle (x,y,z,1){\begin{pmatrix}a_{11}&a_{12}&a_{13}&a_{1}\\a_{21}&a_{22}&a_{23}&a_{2}\\a_{31}&a_{32}&a_{33}&a_{3}\\a_{1}&a_{2}&a_{3}&a_{0}\\\end{pmatrix}}{\begin{pmatrix}x\\y\\z\\1\end{pmatrix}}=0} 其中，对称矩阵 A = ( a i j ) 4 × 4 {\displaystyle A=(a_{ij})_{4\times 4}} 叫做这个曲面方程的矩阵，它是唯一确定的。一次项部分之半常记作这样一个列向量： δ = ( a 1 , a 2 , a 3 ) T . {\displaystyle \delta =(a_{1},a_{2},a_{3})^{\text{T}}.} 因此曲面的矩阵也可写作如下分块矩阵： A = ( A 1 δ δ T a 0 ) {\displaystyle A={\begin{pmatrix}A_{1}&\delta \\\delta ^{\text{T}}&a_{0}\\\end{pmatrix}}}二次曲面的方程中还有以下记号： F 1 ( x , y , z ) = a 11 x + a 12 y + a 13 z + a 1 F 2 ( x , y , z ) = a 21 x + a 22 y + a 23 z + a 2 F 3 ( x , y , z ) = a 31 x + a 32 y + a 33 z + a 3 F 4 ( x , y , z ) = a 1 x + a 2 y + a 3 z + a 0 φ ( x , y , z ) = a 11 x 2 + a 22 y 2 + a 33 z 2 + 2 a 12 x y + 2 a 13 x z + 2 a 23 y z φ 1 ( x , y , z ) = a 11 x + a 12 y + a 13 z φ 2 ( x , y , z ) = a 21 x + a 22 y + a 23 z φ 3 ( x , y , z ) = a 31 x + a 32 y + a 33 z φ 4 ( x , y , z ) = a 1 x + a 2 y + a 3 z {\displaystyle {\begin{aligned}F_{1}(x,y,z)&=a_{11}x+a_{12}y+a_{13}z+a_{1}\\F_{2}(x,y,z)&=a_{21}x+a_{22}y+a_{23}z+a_{2}\\F_{3}(x,y,z)&=a_{31}x+a_{32}y+a_{33}z+a_{3}\\F_{4}(x,y,z)&=a_{1}x+a_{2}y+a_{3}z+a_{0}\\\varphi (x,y,z)&=a_{11}x^{2}+a_{22}y^{2}+a_{33}z^{2}+2a_{12}xy+2a_{13}xz+2a_{23}yz\\\varphi _{1}(x,y,z)&=a_{11}x+a_{12}y+a_{13}z\\\varphi _{2}(x,y,z)&=a_{21}x+a_{22}y+a_{23}z\\\varphi _{3}(x,y,z)&=a_{31}x+a_{32}y+a_{33}z\\\varphi _{4}(x,y,z)&=a_{1}x+a_{2}y+a_{3}z\\\end{aligned}}} 显然有 F ( x , y , z ) = x F 1 ( x , y , z ) + y F 2 ( x , y , z ) + z F 3 ( x , y , z ) + F 4 ( x , y , z ) φ ( x , y , z ) = x φ 1 ( x , y , z ) + y φ 2 ( x , y , z ) + z φ 3 ( x , y , z ) {\displaystyle {\begin{aligned}F(x,y,z)&=xF_{1}(x,y,z)+yF_{2}(x,y,z)+zF_{3}(x,y,z)+F_{4}(x,y,z)\\\varphi (x,y,z)&=x\varphi _{1}(x,y,z)+y\varphi _{2}(x,y,z)+z\varphi _{3}(x,y,z)\\\end{aligned}}} 方程的化简详见二次曲面的化简。 转轴对称矩阵一定可以（相似）对角化，且施加的变换是正交变换，矩阵 A 1 {\displaystyle A_{1}} 经过对角化得到 A 1 ′ {\displaystyle A'_{1}} 。由二次型理论， φ ( x , y , z ) {\displaystyle \varphi (x,y,z)} 总可化为 φ ′ ( x ′ , y ′ , z ′ ) = a 11 ′ x ′ 2 + a 22 ′ y ′ 2 + a 33 ′ z ′ 2 {\displaystyle \varphi '(x',y',z')=a'_{11}x'^{2}+a'_{22}y'^{2}+a'_{33}z'^{2}} 的形式（这一步是消去交叉项的过程，叫做转轴），使得对称矩阵 T − 1 A 1 T {\displaystyle T^{-1}A_{1}T} 成立的正交矩阵 T {\displaystyle T} 就称作转轴施加的转轴矩阵，它对应着几何空间中的坐标轴的旋转。 移轴经过转轴变换，原二次曲面化简为 F ′ ( x ′ , y ′ , z ′ ) = λ 1 x ′ 2 + λ 2 y ′ 2 + λ 3 z ′ 2 + 2 a 1 ′ x ′ + 2 a 2 ′ y ′ + 2 a 3 ′ z ′ + a 0 ′ = 0. {\displaystyle F'(x',y',z')=\lambda _{1}x'^{2}+\lambda _{2}y'^{2}+\lambda _{3}z'^{2}+2a'_{1}x'+2a'_{2}y'+2a'_{3}z'+a'_{0}=0.} 继续通过配方法并分 λ i , i = 1 , 2 , 3 {\displaystyle \lambda _{i},i=1,2,3} 和0的关系的的情况讨论，就可最终化简出曲面方程。 二次曲面的主方向利用特征方程 | λ E − A 1 | = 0 {\displaystyle |\lambda E-A_{1}|=0} 求出的特征根也叫做二次曲面的特征根，在实数范围内，该三次方程一定有三个根（因为 A 1 {\displaystyle A_{1}} 是对称矩阵）， A 1 {\displaystyle A_{1}} 的对应于 λ i , i = 1 , 2 , 3 {\displaystyle \lambda _{i},i=1,2,3} 的特征向量 X i → , i = 1 , 2 , 3 {\displaystyle {\vec {X_{i}}},i=1,2,3} 的方向称为该曲面对应于特征根 λ i {\displaystyle \lambda _{i}} 的主方向。 如果有一个零特征根 λ = 0 {\displaystyle \lambda =0} ，那么就称这个特征根对应的主方向是奇异的，否则就称为非奇异的。二次曲面的特征根不可能全为零，因此该曲面必有一个非奇异主方向。 二次曲面三个特征根所对的主方向总可以化为彼此正交的向量。如果曲面的三个特征根互异，那么该二次曲面的三个主方向已经两两正交了；如果 λ 1 = λ 2 ≠ λ 3 {\displaystyle \lambda _{1}=\lambda _{2}\neq \lambda _{3}} ，且 X 1 → , X 3 → {\displaystyle {\vec {X_{1}}},{\vec {X_{3}}}} 是该曲面的主方向，那么 X 1 → × X 3 → {\displaystyle {\vec {X_{1}}}\times {\vec {X_{3}}}} 是 λ 2 {\displaystyle \lambda _{2}} 对应的主方向；如果 λ = λ 1 = λ 2 = λ 3 {\displaystyle \lambda =\lambda _{1}=\lambda _{2}=\lambda _{3}} ，由于 T − 1 ( λ E ) T = λ E {\displaystyle T^{-1}(\lambda E)T=\lambda E} ，和数量矩阵正交相似的矩阵只能是数量矩阵，因此不用转轴操作（这种情况下原曲面方程中已不含交叉项）。 满足方程 φ ( x , y , z ) = a 11 x 2 + a 22 y 2 + a 33 z 2 + 2 a 12 x y + 2 a 13 x z + 2 a 23 y z = 0 {\displaystyle \varphi (x,y,z)=a_{11}x^{2}+a_{22}y^{2}+a_{33}z^{2}+2a_{12}xy+2a_{13}xz+2a_{23}yz=0} 的方向 v → = ( x , y , z ) T {\displaystyle {\vec {v}}=(x,y,z)^{\text{T}}} 称为这个二次曲面的渐进方向。 二次曲面种类 类型 名称 图像 方程 椭球面 椭球面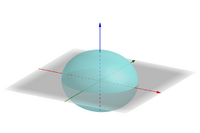
x
2
a
2
+
y
2
b
2
+
z
2
c
2
=
1
{\displaystyle {\dfrac {x^{2}}{a^{2}}}+{\dfrac {y^{2}}{b^{2}}}+{\dfrac {z^{2}}{c^{2}}}=1}
点
\
x
2
a
2
+
y
2
b
2
+
z
2
c
2
=
0
{\displaystyle {\dfrac {x^{2}}{a^{2}}}+{\dfrac {y^{2}}{b^{2}}}+{\dfrac {z^{2}}{c^{2}}}=0}
虚椭球面
\
x
2
a
2
+
y
2
b
2
+
z
2
c
2
=
−
1
{\displaystyle {\dfrac {x^{2}}{a^{2}}}+{\dfrac {y^{2}}{b^{2}}}+{\dfrac {z^{2}}{c^{2}}}=-1}
双曲面
单叶双曲面
x
2
a
2
+
y
2
b
2
−
z
2
c
2
=
1
{\displaystyle {\dfrac {x^{2}}{a^{2}}}+{\dfrac {y^{2}}{b^{2}}}-{\dfrac {z^{2}}{c^{2}}}=1}
双叶双曲面
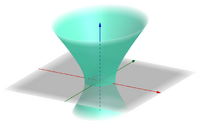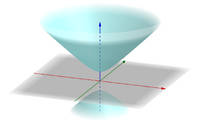x
2
a
2
+
y
2
b
2
−
z
2
c
2
=
−
1
{\displaystyle {\dfrac {x^{2}}{a^{2}}}+{\dfrac {y^{2}}{b^{2}}}-{\dfrac {z^{2}}{c^{2}}}=-1}
抛物面
椭圆抛物面
x
2
p
+
y
2
q
=
2
z
{\displaystyle {\dfrac {x^{2}}{p}}+{\dfrac {y^{2}}{q}}=2z}
双曲抛物面
x
2
p
−
y
2
q
=
2
z
{\displaystyle {\dfrac {x^{2}}{p}}-{\dfrac {y^{2}}{q}}=2z}
二次锥面
二次锥面
x
2
a
2
+
y
2
b
2
−
z
2
c
2
=
0
{\displaystyle {\dfrac {x^{2}}{a^{2}}}+{\dfrac {y^{2}}{b^{2}}}-{\dfrac {z^{2}}{c^{2}}}=0}
二次柱面
椭圆柱面
x
2
a
2
+
y
2
b
2
=
1
{\displaystyle {\dfrac {x^{2}}{a^{2}}}+{\dfrac {y^{2}}{b^{2}}}=1}
虚椭圆柱面
\
x
2
a
2
+
y
2
b
2
=
−
1
{\displaystyle {\dfrac {x^{2}}{a^{2}}}+{\dfrac {y^{2}}{b^{2}}}=-1}
直线
\
x
2
a
2
+
y
2
b
2
=
0
{\displaystyle {\dfrac {x^{2}}{a^{2}}}+{\dfrac {y^{2}}{b^{2}}}=0}
双曲柱面
x
2
a
2
−
y
2
b
2
=
1
{\displaystyle {\dfrac {x^{2}}{a^{2}}}-{\dfrac {y^{2}}{b^{2}}}=1}
一对相交平面
x
2
a
2
−
y
2
b
2
=
0
{\displaystyle {\dfrac {x^{2}}{a^{2}}}-{\dfrac {y^{2}}{b^{2}}}=0}
抛物柱面
x
2
=
2
p
y
{\displaystyle x^{2}=2py}
一对平行平面
x
2
a
2
=
1
{\displaystyle {\dfrac {x^{2}}{a^{2}}}=1}
一对虚平行平面
\
x
2
a
2
=
−
1
{\displaystyle {\dfrac {x^{2}}{a^{2}}}=-1}
一对重合平面
\
x
2
=
0
{\displaystyle x^{2}=0}
|
其中
a
11
,
a
22
,
a
33
,
a
12
,
a
13
,
a
23
{\displaystyle a_{11},a_{22},a_{33},a_{12},a_{13},a_{23}}
不全为零。方程的二次项部分记作
φ
(
x
,
y
,
z
)
=
a
11
x
2
+
a
22
y
2
+
a
33
z
2
+
2
a
12
x
y
+
2
a
13
x
z
+
2
a
23
y
z
{\displaystyle \varphi (x,y,z)=a_{11}x^{2}+a_{22}y^{2}+a_{33}z^{2}+2a_{12}xy+2a_{13}xz+2a_{23}yz}
，这是一个三元二次型，它所对应的矩阵常记为
A
1
=
(
a
i
j
)
3
×
3
=
(
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
)
{\displaystyle A_{1}=(a_{ij})_{3\times 3}={\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{pmatrix}}}
。
其中，对称矩阵
A
=
(
a
i
j
)
4
×
4
{\displaystyle A=(a_{ij})_{4\times 4}}
叫做这个曲面方程的矩阵，它是唯一确定的。一次项部分之半常记作这样一个列向量：
δ
=
(
a
1
,
a
2
,
a
3
)
T
.
{\displaystyle \delta =(a_{1},a_{2},a_{3})^{\text{T}}.}
因此曲面的矩阵也可写作如下分块矩阵：
A
=
(
A
1
δ
δ
T
a
0
)
{\displaystyle A={\begin{pmatrix}A_{1}&\delta \\\delta ^{\text{T}}&a_{0}\\\end{pmatrix}}}
显然有
F
(
x
,
y
,
z
)
=
x
F
1
(
x
,
y
,
z
)
+
y
F
2
(
x
,
y
,
z
)
+
z
F
3
(
x
,
y
,
z
)
+
F
4
(
x
,
y
,
z
)
φ
(
x
,
y
,
z
)
=
x
φ
1
(
x
,
y
,
z
)
+
y
φ
2
(
x
,
y
,
z
)
+
z
φ
3
(
x
,
y
,
z
)
{\displaystyle {\begin{aligned}F(x,y,z)&=xF_{1}(x,y,z)+yF_{2}(x,y,z)+zF_{3}(x,y,z)+F_{4}(x,y,z)\\\varphi (x,y,z)&=x\varphi _{1}(x,y,z)+y\varphi _{2}(x,y,z)+z\varphi _{3}(x,y,z)\\\end{aligned}}}
方程的化简
经过对角化得到
A
1
′
{\displaystyle A'_{1}}
。由二次型理论，
φ
(
x
,
y
,
z
)
{\displaystyle \varphi (x,y,z)}
总可化为
φ
′
(
x
′
,
y
′
,
z
′
)
=
a
11
′
x
′
2
+
a
22
′
y
′
2
+
a
33
′
z
′
2
{\displaystyle \varphi '(x',y',z')=a'_{11}x'^{2}+a'_{22}y'^{2}+a'_{33}z'^{2}}
的形式（这一步是消去交叉项的过程，叫做转轴），使得对称矩阵
T
−
1
A
1
T
{\displaystyle T^{-1}A_{1}T}
成立的正交矩阵
T
{\displaystyle T}
就称作转轴施加的转轴矩阵，它对应着几何空间中的坐标轴的旋转。
继续通过配方法并分
λ
i
,
i
=
1
,
2
,
3
{\displaystyle \lambda _{i},i=1,2,3}
和0的关系的的情况讨论，就可最终化简出曲面方程。
二次曲面的主方向
求出的特征根也叫做二次曲面的特征根，在实数范围内，该三次方程一定有三个根（因为
A
1
{\displaystyle A_{1}}
的方向称为该曲面对应于特征根
λ
i
{\displaystyle \lambda _{i}}
的主方向。
，那么就称这个特征根对应的主方向是奇异的，否则就称为非奇异的。二次曲面的特征根不可能全为零，因此该曲面必有一个非奇异主方向。
，且
X
1
→
,
X
3
→
{\displaystyle {\vec {X_{1}}},{\vec {X_{3}}}}
是该曲面的主方向，那么
X
1
→
×
X
3
→
{\displaystyle {\vec {X_{1}}}\times {\vec {X_{3}}}}
是
λ
2
{\displaystyle \lambda _{2}}
对应的主方向；如果
λ
=
λ
1
=
λ
2
=
λ
3
{\displaystyle \lambda =\lambda _{1}=\lambda _{2}=\lambda _{3}}
，由于
T
−
1
(
λ
E
)
T
=
λ
E
{\displaystyle T^{-1}(\lambda E)T=\lambda E}
，和数量矩阵正交相似的矩阵只能是数量矩阵，因此不用转轴操作（这种情况下原曲面方程中已不含交叉项）。
的方向
v
→
=
(
x
,
y
,
z
)
T
{\displaystyle {\vec {v}}=(x,y,z)^{\text{T}}}
称为这个二次曲面的渐进方向。
二次曲面种类
类型
名称
图像
方程
椭球面
椭球面
点
\
x
2
a
2
+
y
2
b
2
+
z
2
c
2
=
0
{\displaystyle {\dfrac {x^{2}}{a^{2}}}+{\dfrac {y^{2}}{b^{2}}}+{\dfrac {z^{2}}{c^{2}}}=0}
虚椭球面
\
x
2
a
2
+
y
2
b
2
+
z
2
c
2
=
−
1
{\displaystyle {\dfrac {x^{2}}{a^{2}}}+{\dfrac {y^{2}}{b^{2}}}+{\dfrac {z^{2}}{c^{2}}}=-1}
双曲面
单叶双曲面
双叶双曲面
抛物面
椭圆抛物面
双曲抛物面
二次锥面
二次锥面
二次柱面
椭圆柱面
虚椭圆柱面
\
x
2
a
2
+
y
2
b
2
=
−
1
{\displaystyle {\dfrac {x^{2}}{a^{2}}}+{\dfrac {y^{2}}{b^{2}}}=-1}
直线
\
x
2
a
2
+
y
2
b
2
=
0
{\displaystyle {\dfrac {x^{2}}{a^{2}}}+{\dfrac {y^{2}}{b^{2}}}=0}
双曲柱面
一对相交平面
抛物柱面
一对平行平面
一对虚平行平面
\
x
2
a
2
=
−
1
{\displaystyle {\dfrac {x^{2}}{a^{2}}}=-1}
一对重合平面
\
x
2
=
0
{\displaystyle x^{2}=0}
【本文地址】
今日新闻 |
推荐新闻 |